Question

【题目】操作计算．

（1）根据如图完成下列各题．

①把线段比例尺改成数值比例尺是　 　．

②量得AC的长是　 　厘米，AC的实际长度是　 　米．

③量得∠B=　 　度．（精确到十位）

④画出从B点到AC边的最短路线．

⑤求出△ABC的图上面积是　 　平方厘米．

（2）自学下面这段材料，然后回答问题．

我们知道，在整数中“两个数的和等于这两个数的积”的情形并不多，例如2+2=2×2．但是在分数中，这种现象却很普遍．请观察下面的几个例子：

因为：+=4，×=4，所以+=×．

因为：+=4，×=4，所以+=×．

根据以上结果，我们发现了这样的一个规律：两个分数，如果它们的　 　相同，并且　 　，那么这两个分数的和等于它们的积．例如　 　+　 　=　 　×　 　．

Answer 1

【答案】1：3000，3，90，110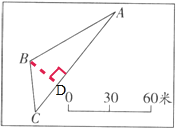，，1.5，分子，分母相差1，如，，，

【解析】

试题分析：（1）①比例尺=图上距离：实际距离，据此线段比例尺转化成数值比例尺；

②量得AC的长是3厘米，用3乘30即可求出AC的实际长度；

③用量角器量得∠B=110度；

④从B点到AC边作垂线就是从B点到AC边的最短路线；

⑤利用三角形的面积公式S=ah÷2求出三角形的面积；

（2）观察给出的式子发现：两个分数，如果它们的分子相同，并且分母相差1，那么这两个分数的和等于它们的积．例如+=×．

解：（1）1厘米：30米=1厘米：3000厘米=1：3000，

②量得AC的长是3厘米，用3×30=90（米），

③用量角器量得∠B=110度；

④从B点到AC边作垂线就是从B点到AC边的最短路线；

如图：

⑤AD=1厘米，

3×1÷2=1.5（平方厘米），

（2）观察给出的式子发现：两个分数，如果它们的分子相同，并且分母相差1，那么这两个分数的和等于它们的积．例如+=×．

故答案为：1：3000，3，90，110，1.5，分子，分母相差1，如，，，．