
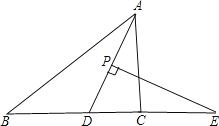
【题目】如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
(1)若∠B=30°,∠ACB=80°,求∠E的度数;
(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.
【答案】(1)∠E=25°;(2)∠E=![]() (∠ACB﹣∠B).
(∠ACB﹣∠B).
【解析】
(1)首先根据三角形的内角和定理求得∠BAC的度数,再根据角平分线的定义求得∠DAC的度数,从而根据三角形的内角和定理即可求出∠ADC的度数,进一步求得∠E的度数;
(2)根据第(1)小题的思路即可推导这些角之间的关系.
解:(1)∵∠B=30°,∠ACB=80°,
∴∠BAC=70°,
∵AD平分∠BAC,
∴∠DAC=35°,
∴∠ADC=65°,
∴∠E=25°;
(2)∠E=![]() (∠ACB﹣∠B).
(∠ACB﹣∠B).
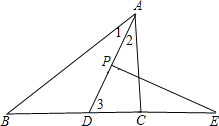
设∠B=n°,∠ACB=m°,
∵AD平分∠BAC,
∴∠1=∠2=![]() ∠BAC,
∠BAC,
∵∠B+∠ACB+∠BAC=180°,
∵∠B=n°,∠ACB=m°,
∴∠CAB=(180-n-m)°,
∴∠BAD=![]() (180-n-m)°,
(180-n-m)°,
∴∠3=∠B+∠1=n°+![]() (180-n-m)°=90°+
(180-n-m)°=90°+![]() n°-
n°-![]() m°,
m°,
∵PE⊥AD,
∴∠DPE=90°,
∴∠E=90°-(90°+![]() n°-
n°-![]() m°)=
m°)=![]() (m-n)°=
(m-n)°=![]() (∠ACB-∠B).
(∠ACB-∠B).


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
【题目】某学校在暑假期间开展“心怀感恩,孝敬父母”的实践活动,倡导学生在假期中帮助父母干家务,开学以后,校学生会随机抽取了部分学生,就暑假“平均每天帮助父母干家务所用时长”进行了调查,以下是根据相关数据绘制的统计图的部分:

根据上述信息,回答下列问题:
![]() 在本次随机抽取的样本中,调查的学生人数是 人;
在本次随机抽取的样本中,调查的学生人数是 人;
![]()
![]() ,
,![]() ;
;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 如果该校共有学生
如果该校共有学生![]() 人,请你估计“平均每天帮助父母干家务的时长不少于
人,请你估计“平均每天帮助父母干家务的时长不少于![]() 分钟”的学生大约有多少人?
分钟”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点![]() 按如图所示的方式叠放在一起(其中
按如图所示的方式叠放在一起(其中![]() ,
,![]() ,
,![]() ),固定三角板
),固定三角板![]() ,另一三角板
,另一三角板![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 顺时针旋转,设旋转的角度为
顺时针旋转,设旋转的角度为![]() .
.
(1)当![]() 时;
时;
①若![]() ,则
,则![]() 的度数为 ;
的度数为 ;
②若![]() ,求
,求![]() 的度数;
的度数;
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)当![]() 时,这两块三角尺是否存在一组边互相垂直?若存在,请直接写出
时,这两块三角尺是否存在一组边互相垂直?若存在,请直接写出![]() 所有可能的值,并指出哪两边互相垂直(不必说明理由);若不存在,请说明理由.
所有可能的值,并指出哪两边互相垂直(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
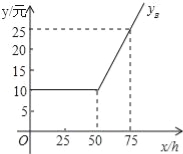
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
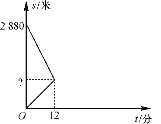
【题目】五一假期过后,小明到校后发现忘记带数学课本,一看手表,离上课还有20分钟,他立刻步行返回家中取书,同时,他的父亲也发现小明忘记带数学课本,带上课本立刻以小明步行速度的2倍骑车赶往学校.父子在途中相遇,小明拿到课本后马上按原速步行返回学校,到校后发现迟到了4分钟.如图是父子俩离学校的路程s(米)与所用时间t(分)之间的函数关系,请结合图像,回答下列问题:
(1)两人相遇处离学校的距离是多少米?
(2)试求小明的父亲在赶往学校的过程中,路程s与时间t之间的函数表达式;
(3)假如小明父子相遇拿到课本后,改由他的父亲骑车搭他到学校,他会迟到吗?如果会,迟到几分钟;如果不会,能提前几分钟到校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PGH的面积和等于 . 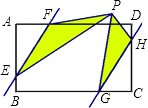
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知2x﹣1的平方根是±6,2x+y﹣1的算术平方根是5,求2x﹣3y+11的立方根.
(2)已知x是1的平方根,求代数式(x2017﹣1)(x2018﹣712)(x2019+1)(x2020+712)+1000x的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1所示,(单位:cm)
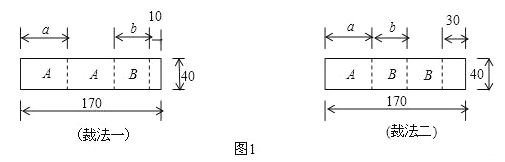
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
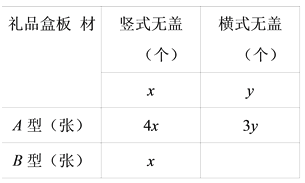
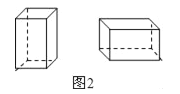
③做成的竖式和横式两种无盖礼品盒总数最多是 个;此时,横式无盖礼品盒可以做 个.(在横线上直接写出答案,无需书写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是三角形外一动点,满足∠ADB=600,
(1)当D点在AC的垂直平分线上时,求证: DA+DC=DB.
(2)当D点不在AC的垂直平分线上时,(1)中的结论是否仍然成立?请说明理由.
(3)当D点在如图的位置时,直接写出DA,DC,DB的数量关系,不必证明.
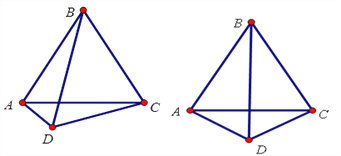
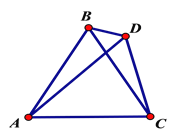
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com