
����Ŀ������ij��װ������ҵ�н���һ���Ϻ����������Ʒ������ҵ����Ϊ��ȷ������������ҵ���������������ǹ��ù����170cm��40cm�ı������Ϊԭ������ÿ�ű�����ٰ��ղ÷�һ��÷�������A����B�����ְ�ģ���ͼ1��ʾ������λ��cm��
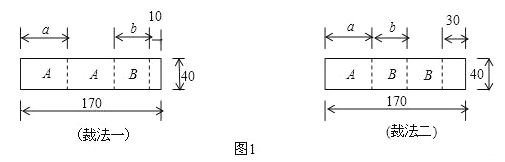
��1���г����̣����������ͼ����a��b��ֵ��
��2������������������30�ű�����ò÷�һ�ü���4�ű�����ò÷����ü����ٽ��õ���A����B�Ͱ��������͵���������ͼ2����ʽ���ʽ��������Ʒ����
�����ֲ÷�������A�Ͱ���� ������B�Ͱ���� ������
�������ɵ���ʽ����Ʒ��x������ʽ����Ʒ�е�y��������������ɱ�����
�����ɵ���ʽ�ͺ�ʽ��������Ʒ������������� ��������ʱ����ʽ����Ʒ�п������� ���������ں�����ֱ��д������������д������
���𰸡���1��a=60��b=40����2����64��38����2y����20��16��17��18��
��������
��1����ͼʾ�г�����a��b�Ķ�Ԫһ�η��������;
��2��������֪��ͼʾ��������ֲ÷�������A�Ͱ�ĺ�B�Ͱ�ĵ�������ͬ����ͼʾ��ɱ�����ɼ��㣮
��1��������ã�![]() ����ã�
����ã�![]() ��
��
��ͼ����a��b��ֵ�ֱ�Ϊ��60��40��
��2������ͼʾ�÷�һ����A�Ͱ��Ϊ��2��30��60���÷�������A�Ͱ��Ϊ��1��4��4���������ֲ÷�������A�Ͱ��
Ϊ60+4��64���ţ�����ͼʾ�÷�һ����B�Ͱ��Ϊ��1��30��30���÷�������A�Ͱ��Ϊ��2��4��8���������ֲ÷�������B�Ͱ��
Ϊ30+8��38���ţ���
�ʴ�Ϊ��64��38��
������֪��ͼʾ�ã���ʽ����Ʒ�е�y����ÿ����Ʒ����2��B�Ͱ�ģ�������B�Ͱ��2y�ţ�
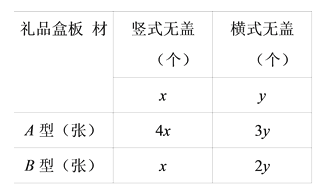
�����ϱ���֪��ʽ�ǿ�ʽ��5y���棬��A��3y�ţ���B����Ҫ2y�ţ�
����������ӹ���ҪA��4x+3y�ţ�B��x+2y�ţ�
��4x+3y��64��x+2y��38����ʽ��ӵ�5x+5y��102��
��x+y��20.4�����������20����
��ʽ�����3x+y��26����2x��5.6�����x��2.8����y��18��
���ʽ����16��17��18����
�ʴ�Ϊ��20��16��17��18��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
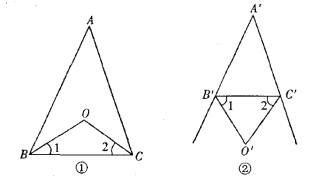
����Ŀ��(1)��ͼ�٣�����ABC�У���ABC����ACB��ƽ�����ཻ�ڵ�O����A=40�������BOC�Ķ�����
(2)��ͼ�ڣ���A��B��C�������ƽ�����ཻ�ڵ�O������A��=40�������B��O��C���Ķ�����
(3)����(1)(2)�����еġ�BOC���B��O��C�� ��������������ϵ?����A=��A��=n������BOC���B��O��C�� �Ƿ��������Ĺ�ϵ?����������������õ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
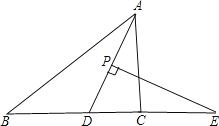
����Ŀ����ͼ���ڡ�ABC�У�ADƽ�֡�BAC��PΪ�߶�AD�ϵ�һ�����㣬PE��AD��ֱ��BC�ڵ�E��
��1������B��30�㣬��ACB��80�㣬���E�Ķ�����
��2����P�����߶�AD���˶�ʱ�������E���B����ACB��������ϵ��д����������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������
��1�����㣺��22+ ![]() ��2cos60��+|��3|��
��2cos60��+|��3|��
��2���ⲻ��ʽ�飺 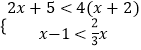 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ͷ�����Թ涨����6������Ϊ�ϸ�9������Ϊ���㣬�ס�������ͬѧ��һ�β��Գɼ����£�
�ɼ����֣� | 4 | 5 | 6 | 7 | 8 | 9 |
���飨�ˣ� | 1 | 2 | 5 | 2 | 1 | 4 |
���飨�ˣ� | 1 | 1 | 4 | 5 | 2 | 2 |
��1�������������ͳ�����ݣ��������ͼ�ͱ����������� 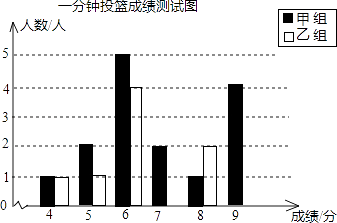
һ����Ͷ���ɼ�ͳ�Ʒ�������
ͳ���� | ƽ���� | ���� | ��λ�� | �ϸ��� | ������ |
���� | 2.56 | 6 | 80.0% | 26.7% | |
���� | 6.8 | 1.76 | 86.7% | 13.3% |
��2��������С����С�ϵ�һ�ζԻ���������ݣ�1���еı���д������֧��С�ϵĹ۵�����ɣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
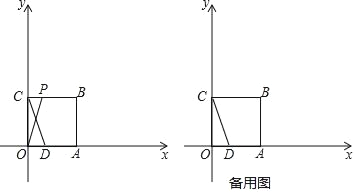
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬������OABC�Ķ���A��C�ֱ���x����y���ϣ���֪�����α߳�Ϊ3����DΪx����һ�㣬������Ϊ��1��0��������CD����P�ӵ�C������ÿ��1����λ���ٶ�������C��B��A�ķ������յ�A�˶�������P���A�غ�ʱֹͣ�˶����˶�ʱ��Ϊt�룮
��1������OP������P���߶�BC���˶�����������CPO�ա�ODCʱ����ֱ��OP�ı���ʽ��
��2������PC������CPD�����S����t�ĺ�������ʽ��
��3����P���˶������У��Ƿ����ij��λ��ʹ����CDPΪ���������Σ������ڣ�ֱ��д����P�����꣬�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC���������������ϣ�����AC��������y=x2��4x��2����A��B���㣮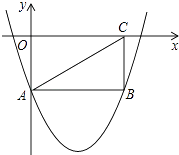
��1����A�����꼰�߶�AB�ij���
��2������P�ɵ�A������ÿ��1����λ���ٶ���AB�����B�ƶ���1����QҲ�ɵ�A������ÿ��7����λ���ٶ���AO��OC��CB�����B�ƶ���������һ���㵽���յ�ʱ��һ����Ҳֹͣ�ƶ�����P���ƶ�ʱ��Ϊt�룮
�ٵ�PQ��ACʱ����t��ֵ��
�ڵ�PQ��ACʱ�����������߶Գ�����һ��H����HOQ����POQ�����H���������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ�����ͼ����A��-6��4����B��3��0����
��1������������Ľ���ʽ��
��2���������������ͼ��
��3������ֱ�߾����㣨9��m������m��ֵ��
��4�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����EF�С�O�ڵ�D������B��BH��EF�ڵ�H������O�ڵ�C������BD�� 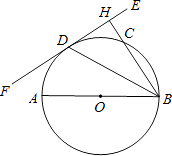
��1����֤��BDƽ�֡�ABH��
��2�����AB=12��BC=8����Բ��O��BC�ľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com