
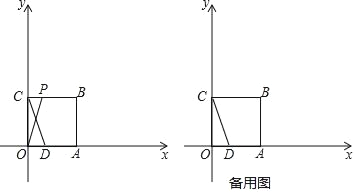
【题目】如图,在平面直角坐标系中,O是坐标原点,正方形OABC的顶点A、C分别在x轴与y轴上,已知正方形边长为3,点D为x轴上一点,其坐标为(1,0),连接CD,点P从点C出发以每秒1个单位的速度沿折线C→B→A的方向向终点A运动,当点P与点A重合时停止运动,运动时间为t秒.
(1)连接OP,当点P在线段BC上运动,且满足△CPO≌△ODC时,求直线OP的表达式;
(2)连接PC,求△CPD的面积S关于t的函数表达式;
(3)点P在运动过程中,是否存在某个位置使得△CDP为等腰三角形,若存在,直接写出点P的坐标,若不存在,说明理由.
【答案】(1)y=3x;(2)S=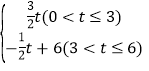 ;(3)满足条件的点P坐标为(2,3)或(3,
;(3)满足条件的点P坐标为(2,3)或(3,![]() )或(3,2)或(3,
)或(3,2)或(3,![]() ).
).
【解析】
(1) 四边形ABCO是正方形, 可得COD=∠OCP, OC=CO继而证明△CPO≌△ODC, 可得P点坐标,即可确定OP解析式;
(2) 分当点P在线段BC上时,当点P在线段AB上时两种情况讨论即可;
(3) 存在, 分别以DC=DP1, DC=DP2, CD=CP3, P4C=P4D四种情况考虑, 利用勾股定理及图形与坐标性质求出P坐标即可.
(1)∵四边形ABCO是正方形,
∴∠COD=∠OCP,∵OC=CO,
∴当CP=OD=1时,△CPO≌△ODC,
∴P(1,3),
设直线OP的解析式为y=kx,则有3=k,
∴直线OP的解析式为y=3x.
(2)当点P在线段BC上时,如图1中,
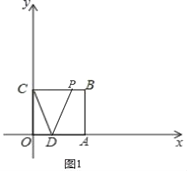
S=![]() CPCO=
CPCO=![]() t(0<t≤3),
t(0<t≤3),
当点P在线段AB上时,如图2中,
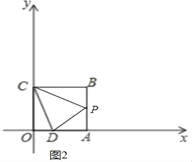
BP=t﹣3,AP=3﹣(t﹣3)=6﹣t,
S=3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×3×(t﹣3)﹣
×3×(t﹣3)﹣![]() ×2×(6﹣t)=﹣
×2×(6﹣t)=﹣![]() t=6(3<t≤6),
t=6(3<t≤6),
综上所述,S=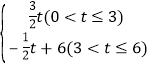 .
.
(3)如图3中,
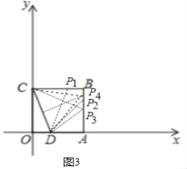
①当DC=DP1时,P1(2,3),
②当DC=DP2时,AP2=![]() =
=![]() ,
,
∴P2(3,![]() ).
).
③当CD=CP3=![]() 时,BP3=
时,BP3=![]() =1,
=1,
∴P3(3,2).
④当P4C=P4D时,设AP4=a,
则有22+a2=32+(3﹣a)2,
解得a=![]() ,
,
∴P4(3,![]() ),
),
综上所述,满足条件的点P坐标为(2,3)或(3,![]() )或(3,2)或(3,
)或(3,2)或(3,![]() ).
).


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:

(1)如果校方认为教师的教学技能水平与专业知识水平同等重要,那么候选人 将被录取.
(2)如果校方认为教师的教学技能水平比专业知识水平重要,并分别赋予它们6和4的权.计算他们赋权后各自的平均成绩,并说明谁将被录取.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PGH的面积和等于 . 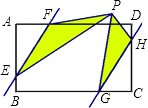
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°.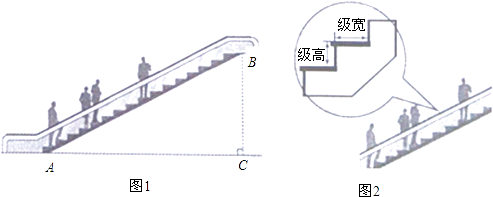
(1)求一楼与二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米(精确到0.01米)?备用数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1所示,(单位:cm)
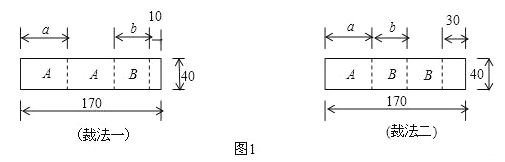
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
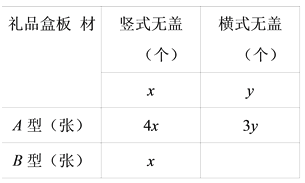
③做成的竖式和横式两种无盖礼品盒总数最多是 个;此时,横式无盖礼品盒可以做 个.(在横线上直接写出答案,无需书写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

查看答案和解析>>
科目:初中数学 来源: 题型:
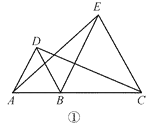
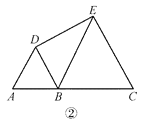
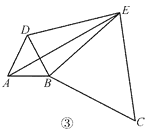
【题目】在直线上顺次取 A,B,C 三点,分别以 AB,BC 为边长在直线的同侧作正三角形, 作得两个正三角形的另一顶点分别为 D,E.
(1)如图①,连结 CD,AE,求证:CD=AE;
(2)如图②,若 AB=1,BC=2,求 DE 的长;
(3)如图③,将图②中的正三角形 BCE 绕 B 点作适当的旋转,连结 AE,若有 DE2+BE2= AE2,试求∠DEB 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2 ![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 . 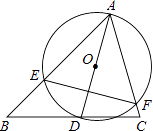
查看答案和解析>>
科目:初中数学 来源: 题型:
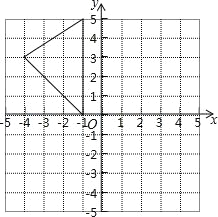
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com