
����Ŀ��ijУΪ����Ƹһ�������ʦ������ѡ��������ѡ�˽��н�ѧ������רҵ֪ʶ���ֿ������ֽ��������������˵Ŀ��˳ɼ�ͳ��������

��1�����У����Ϊ��ʦ�Ľ�ѧ����ˮƽ��רҵ֪ʶˮƽͬ����Ҫ����ô��ѡ��������������¼ȡ��
��2�����У����Ϊ��ʦ�Ľ�ѧ����ˮƽ��רҵ֪ʶˮƽ��Ҫ�����ֱ�������6��4��Ȩ���������Ǹ�Ȩ����Ե�ƽ���ɼ�����˵��˭����¼ȡ��
���𰸡���1��������2���ҽ���¼ȡ��
��������
��1������ƽ�����ļ��㹫ʽ�ֱ������ס��ҡ�����ƽ�������ٽ��бȽϣ����ɵó��𰸣�
��2�����������������6��4�ļס��ҡ�����ƽ�������ٽ��бȽϣ����ɵó��𰸣�
��1����ƽ�����ǣ���85+92����2=88.5���֣���
�ҵ�ƽ�����ǣ���91+85����2=88���֣���
����ƽ�����ǣ���80+90����2=85���֣���
��ƽ���ɼ���ߣ�
���ѡ�˼���¼ȡ��
�ʴ�Ϊ������
��2����������ã���ƽ���ɼ�Ϊ����85��6+92��4����10=87.8���֣���
�ҵ�ƽ���ɼ�Ϊ����91��6+85��4����10=88.6���֣���
����ƽ���ɼ�Ϊ����80��6+90��4����10=84���֣���
��Ϊ�ҵ�ƽ��������ߣ�
�����ҽ���¼ȡ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��һ·�����й�����������ܣ�����ŷ��·��Ϊ�˰�ȫ�����ij����·����������������ת̽�յƣ���ͼ1��ʾ����A���ߴ�AM��ʼ˳ʱ����ת��AN��������ת����B���ߴ�BP��ʼ˳ʱ����ת��BQ��������ת�����Ʋ�ͣ��������Ѳ�ӣ�����Aת�����ٶ���ÿ��2�ȣ���Bת�����ٶ���ÿ��1�ȣ��ٶ�����·��ƽ�еģ���PQ��MN������BAM����BAN=2��1��
��1����գ���BAN=_____�㣻
��2������B������ת��30�룬��A���߲ſ�ʼת�����ڵ�B���ߵ���BQ֮ǰ��A��ת�����룬���ƵĹ�������ƽ�У�
��3����ͼ2��������ͬʱת�����ڵ�A���ߵ���AN֮ǰ��������Ĺ������ڵ�C����C����ACD��PQ�ڵ�D������ACD=120�㣬����ת�������У���̽����BAC����BCD��������ϵ�Ƿ����仯�������䣬�������������ϵ�����ı䣬��˵�����ɣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�E��F��G��H�����Ǹ����е㣬O������һ�㣬���ı���AEOH���ı���BFOE���ı���CGOF������ֱ���4��5��6,���ı���DHOG�������( )
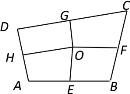
A. 5B. 4C. 8D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��ͼ���ǰ����淽�����Ӷ��ɵģ���0��0������2��0������1��0������0����1������1��1������1����2������1��0������2����1����
��1��������ͼ��������һ��ʲô���֣�
��2���������ͼ������y�����Գ�ͼ�Σ���д����ͼ����Ӧ���˵�����꣬��õ�һ��ʲô���֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
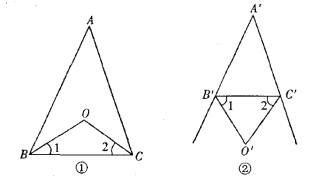
����Ŀ��(1)��ͼ�٣�����ABC�У���ABC����ACB��ƽ�����ཻ�ڵ�O����A=40�������BOC�Ķ�����
(2)��ͼ�ڣ���A��B��C�������ƽ�����ཻ�ڵ�O������A��=40�������B��O��C���Ķ�����
(3)����(1)(2)�����еġ�BOC���B��O��C�� ��������������ϵ?����A=��A��=n������BOC���B��O��C�� �Ƿ��������Ĺ�ϵ?����������������õ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016����ʡ�����У���ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ���A��0��1����B��3��2����C��1��4����������������ĸ���ϣ�
��1��������ABC����x��ĶԳ�ͼ����A1B1C1��
��2������A1B1C1��x�᷽������ƽ��3����λ��õ���A2B2C2��д������A2��B2��C2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��x2+2x+2
��1����������ߵĶԳ��ᡢ���������Լ�y��x�仯�����
��2������ͼ��ֱ������ϵ�ڻ����������ߵ�ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=�� ![]() x2��
x2�� ![]() x+2��x�ύ��A��B���㣬��y�ύ�ڵ�C
x+2��x�ύ��A��B���㣬��y�ύ�ڵ�C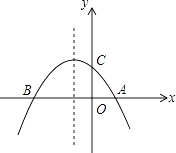
��1�����A��B��C�����ꣻ
��2����E�Ǵ��������ϵĵ㣬��F����Գ����ϵĵ㣬����A��B��E��FΪ�����ƽ���ı��ε������
��3���������ߵĶԳ������Ƿ���ڵ�M��ʹ�á�ACM�ǵ��������Σ������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
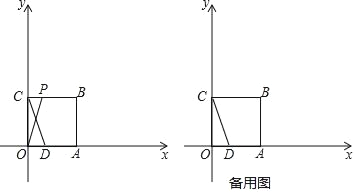
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬������OABC�Ķ���A��C�ֱ���x����y���ϣ���֪�����α߳�Ϊ3����DΪx����һ�㣬������Ϊ��1��0��������CD����P�ӵ�C������ÿ��1����λ���ٶ�������C��B��A�ķ������յ�A�˶�������P���A�غ�ʱֹͣ�˶����˶�ʱ��Ϊt�룮
��1������OP������P���߶�BC���˶�����������CPO�ա�ODCʱ����ֱ��OP�ı���ʽ��
��2������PC������CPD�����S����t�ĺ�������ʽ��
��3����P���˶������У��Ƿ����ij��λ��ʹ����CDPΪ���������Σ������ڣ�ֱ��д����P�����꣬�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com