
【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C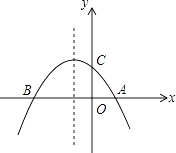
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】
(1)解:令y=0得﹣ ![]() x2﹣
x2﹣ ![]() x+2=0,
x+2=0,
∴x2+2x﹣8=0,
x=﹣4或2,
∴点A坐标(2,0),点B坐标(﹣4,0),
令x=0,得y=2,∴点C坐标(0,2)
(2)解:①由图象AB为平行四边形的边时,
∵AB=EF=6,对称轴x=﹣1,
∴点E的横坐标为﹣7或5,
∴点E坐标(﹣7,﹣ ![]() )或(5,﹣
)或(5,﹣ ![]() ),此时点F(﹣1,﹣
),此时点F(﹣1,﹣ ![]() ),
),
∴以A,B,E,F为顶点的平行四边形的面积=6× ![]() =
= ![]() .
.
②当点E在抛物线顶点时,点E(﹣1, ![]() ),设对称轴与x轴交点为M,令EM与FM相等,则四边形AEBF是菱形,此时以A,B,E,F为顶点的平行四边形的面积=
),设对称轴与x轴交点为M,令EM与FM相等,则四边形AEBF是菱形,此时以A,B,E,F为顶点的平行四边形的面积= ![]() ×6×
×6× ![]() =
= ![]()
(3)解:如图所示,①当C为等腰三角形的顶角的顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,
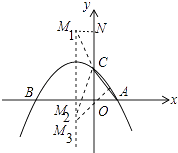
在RT△CM1N中,CN= ![]() =
= ![]() ,
,
∴点M1坐标(﹣1,2+ ![]() ),点M2坐标(﹣1,2﹣
),点M2坐标(﹣1,2﹣ ![]() ).
).
②当M3为等腰三角形的顶角的顶点时,∵直线AC解析式为y=﹣x+2,
∴线段AC的垂直平分线为y=x与对称轴的交点为M3(﹣1.﹣1),
∴点M3坐标为(﹣1,﹣1).
③当点A为等腰三角形的顶角的顶点的三角形不存在.
综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+ ![]() )或(﹣1,2﹣
)或(﹣1,2﹣ ![]() ).
).
【解析】(1)根据抛物线与x轴交于A、B两点,与y轴交于点C,得到点A坐标(2,0),点B坐标(﹣4,0),令x=0,得y=2,得到点C坐标(0,2);(2)①由图象AB为平行四边形的边时,AB=EF=6,对称轴x=﹣1,得到点E的横坐标为﹣7或5,求出点F的坐标,以A,B,E,F为顶点的平行四边形的面积=6×![]() =
=![]() ;②当点E在抛物线顶点时,点E(﹣1,
;②当点E在抛物线顶点时,点E(﹣1,![]() ),设对称轴与x轴交点为M,令EM与FM相等,则四边形AEBF是菱形,此时以A,B,E,F为顶点的平行四边形的面积=
),设对称轴与x轴交点为M,令EM与FM相等,则四边形AEBF是菱形,此时以A,B,E,F为顶点的平行四边形的面积= ![]() ×6×
×6×![]() =
=![]() ;(3)①当C为等腰三角形的顶角的顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,在RT△CM1N中,CN=
;(3)①当C为等腰三角形的顶角的顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,在RT△CM1N中,CN=![]() ,所以点M1坐标(﹣1,2+
,所以点M1坐标(﹣1,2+![]() ),点M2坐标(﹣1,2﹣
),点M2坐标(﹣1,2﹣![]() );②当M3为等腰三角形的顶角的顶点时,因为直线AC解析式为y=﹣x+2,得到线段AC的垂直平分线为y=x与对称轴的交点为M3(﹣1.﹣1),点M3坐标为(﹣1,﹣1);③当点A为等腰三角形的顶角的顶点的三角形不存在;综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+ )或(﹣1,2﹣
);②当M3为等腰三角形的顶角的顶点时,因为直线AC解析式为y=﹣x+2,得到线段AC的垂直平分线为y=x与对称轴的交点为M3(﹣1.﹣1),点M3坐标为(﹣1,﹣1);③当点A为等腰三角形的顶角的顶点的三角形不存在;综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+ )或(﹣1,2﹣![]() ).
).![]()
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


科目:初中数学 来源: 题型:
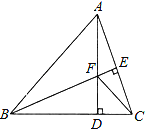
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了招聘一名优秀教师,对入选的三名候选人进行教学技能与专业知识两种考核,现将甲、乙、丙三人的考核成绩统计如下:

(1)如果校方认为教师的教学技能水平与专业知识水平同等重要,那么候选人 将被录取.
(2)如果校方认为教师的教学技能水平比专业知识水平重要,并分别赋予它们6和4的权.计算他们赋权后各自的平均成绩,并说明谁将被录取.
查看答案和解析>>
科目:初中数学 来源: 题型:
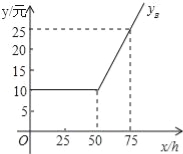
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PGH的面积和等于 . 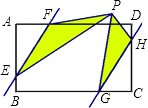
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°.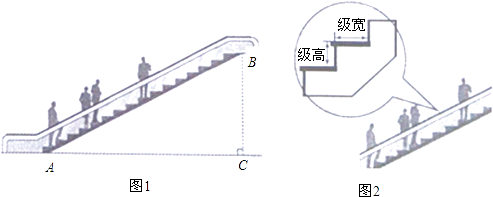
(1)求一楼与二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米(精确到0.01米)?备用数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2 ![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 . 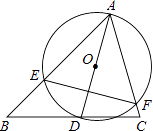
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com