
【题目】如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°.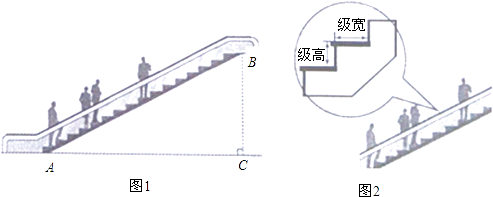
(1)求一楼与二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米(精确到0.01米)?备用数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249.
【答案】
(1)
解:sin∠BAC= ![]() ,
,
∴BC=AB×sin32°
=16.50×0.5299≈8.74米
(2)
解:∵tan32°= ![]() ,
,
∴级高=级宽×tan32°=0.25×0.6249=0.156225
∵10秒钟电梯上升了20级,
∴小明上升的高度为:20×0.156225≈3.12米
【解析】(1)在直角三角形ABC中利用∠BAC的正弦值和AB的长求得BC的长即可;(2)首先根据题意求得级高,然后根据10秒钟上升的级数求小明上升的高度即可.
【考点精析】认真审题,首先需要了解关于坡度坡角问题(坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA).


科目:初中数学 来源: 题型:
【题目】已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C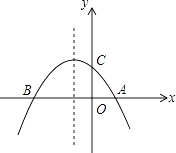
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=BD=BC.在BC延长线上取点C1,连接DC1,使DC=CC1,在CC1延长线上取点C2,在DC1上取点E,使EC1=C1C2,同理FC2=C2C3,若继续如此下去直到Cn,则∠Cn的度数为____.(结果用含![]() 的代数式表示)
的代数式表示)
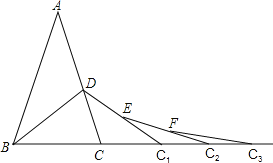
查看答案和解析>>
科目:初中数学 来源: 题型:
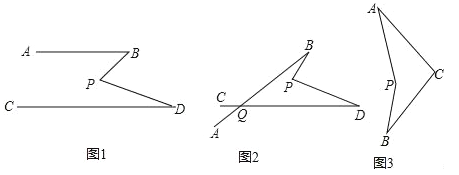
【题目】(1)如图1,若AB∥CD,将点P在AB、CD内部,∠B,∠D,∠P满足的数量关系是 ,并说明理由.
(2)在图1中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图2,利用(1)中的结论(可以直接套用),求∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?
(3)科技活动课上,雨轩同学制作了一个图(3)的“飞旋镖”,经测量发现∠PAC=30°,∠PBC=35°,他很想知道∠APB与∠ACB的数量关系,你能告诉他吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
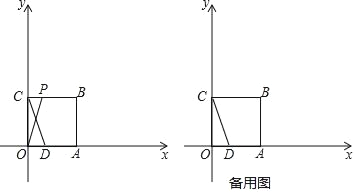
【题目】如图,在平面直角坐标系中,O是坐标原点,正方形OABC的顶点A、C分别在x轴与y轴上,已知正方形边长为3,点D为x轴上一点,其坐标为(1,0),连接CD,点P从点C出发以每秒1个单位的速度沿折线C→B→A的方向向终点A运动,当点P与点A重合时停止运动,运动时间为t秒.
(1)连接OP,当点P在线段BC上运动,且满足△CPO≌△ODC时,求直线OP的表达式;
(2)连接PC,求△CPD的面积S关于t的函数表达式;
(3)点P在运动过程中,是否存在某个位置使得△CDP为等腰三角形,若存在,直接写出点P的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车制造厂开发了一款新式自行车,计划6月份生产安装600辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人:他们经过培训后也能独立进行安装.调研部门发现:1名热练工和2名新工人每日可安装8辆自行车;2名熟练工和3名新工人每日可安装14辆自行车.
(1)每名熟练工和新工人每日分别可以安装多少辆自行车?
(2)如果工厂招聘n名新工人(0<n<10).使得招聘的新工人和抽调熟练工刚好能完成6月份(30天) 的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)该自行车关于轮胎的使用有以下说明:本轮胎如安装在前轮,安全行使路程为11千公里;如安装在后轮,安全行使路程为9千公里.请问一对轮胎能行使的最长路程是多少千公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a厘米的正方形的四个角各剪去一个边长为b厘米的小正方形.
(1)用代数式表示剩余部分的面积;
(2)当a=8.68,b=0.66时,求剩余部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com