
【题目】计算下面各题
(1)计算:﹣22+ ![]() ﹣2cos60°+|﹣3|;
﹣2cos60°+|﹣3|;
(2)解不等式组: 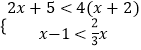 .
.
【答案】
(1)解:﹣22+( ![]() )﹣1﹣2cos60°+|﹣3|,
)﹣1﹣2cos60°+|﹣3|,
=﹣4+3﹣2× ![]() +3,
+3,
=﹣4+3﹣1+3,
=﹣5+6,
=1;
(2)解: 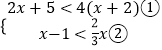
解不等式①,得2x+5<4x+8,
解得x>﹣ ![]() ,
,
解不等式②,得3x﹣3<2x,
解得x<3,
所以,原不等式组的解集是﹣ ![]() <x<3
<x<3
【解析】(1)根据有理数的乘方运算,有理数的负整数指数次幂等于正整数指数次幂的倒数,60°角的余弦值等于 ![]() ,绝对的性质计算即可得解;(2)先求出两个不等式的解集,再求其公共解.
,绝对的性质计算即可得解;(2)先求出两个不等式的解集,再求其公共解.
【考点精析】本题主要考查了整数指数幂的运算性质和一元一次不等式组的解法的相关知识点,需要掌握aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数);解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
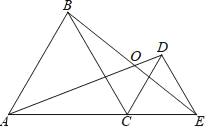
【题目】如图,△ABC和△CDE都是等边三角形,A、C、E在一条直线上.
(1)线段AD与BE相等吗?请证明你的结论;
(2)设AD与BE交于点O,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
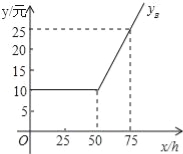
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E,G,H,F分别在AB,BC,CD,AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE,PF,PG,PH,则△PEF和△PGH的面积和等于 . 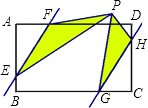
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知2x﹣1的平方根是±6,2x+y﹣1的算术平方根是5,求2x﹣3y+11的立方根.
(2)已知x是1的平方根,求代数式(x2017﹣1)(x2018﹣712)(x2019+1)(x2020+712)+1000x的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°.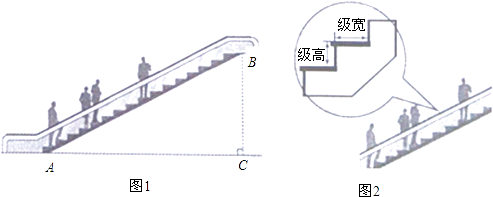
(1)求一楼与二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米(精确到0.01米)?备用数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1所示,(单位:cm)
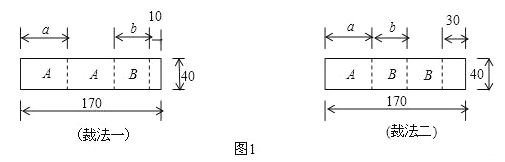
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
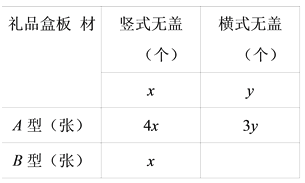
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
③做成的竖式和横式两种无盖礼品盒总数最多是 个;此时,横式无盖礼品盒可以做 个.(在横线上直接写出答案,无需书写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
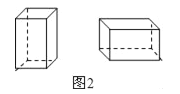
【题目】在直线上顺次取 A,B,C 三点,分别以 AB,BC 为边长在直线的同侧作正三角形, 作得两个正三角形的另一顶点分别为 D,E.
(1)如图①,连结 CD,AE,求证:CD=AE;
(2)如图②,若 AB=1,BC=2,求 DE 的长;
(3)如图③,将图②中的正三角形 BCE 绕 B 点作适当的旋转,连结 AE,若有 DE2+BE2= AE2,试求∠DEB 的度数.
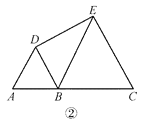
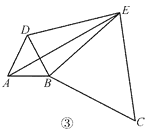
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com