
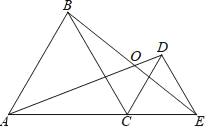
【题目】如图,△ABC和△CDE都是等边三角形,A、C、E在一条直线上.
(1)线段AD与BE相等吗?请证明你的结论;
(2)设AD与BE交于点O,求∠AOE的度数.
【答案】(1)AD=BE;(2)120°.
【解析】
(1) 利用等边三角形的性质得到一对角相等,一对边相等,利用等式的性质得到夹角相等,利用SAS得到三角形ACD与三角形BCE全等,利用全等三角形的对应边相等即可得证.
(2)利用三角形全等,转化相关角度即可解答.
解:(1)AD=BE,
理由如下:在等边△ABC和等边△CDE中,
∵∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ACB=∠CBE+∠AEB=60°,
∴∠CAD+∠AEB=60°,
∴∠AOE=180°﹣(∠CAD+∠AEB)=120°.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若![]() ,则(x)=n.如(0.46)=0,(3.67)=4.
,则(x)=n.如(0.46)=0,(3.67)=4.
给出下列关于(x)的结论:
①(1.493)=1;
②(2x)=2(x);
③若(![]() )=4,则实数x的取值范围是9≤x<11;
)=4,则实数x的取值范围是9≤x<11;
④当x≥0,m为非负整数时,有(m+2019x)=m+(2019x);
⑤(x+y)=(x)+(y);
其中,正确的结论有__________(填写所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
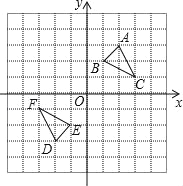
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
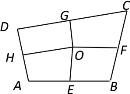
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别是4、5、6,则四边形DHOG的面积是( )
A. 5B. 4C. 8D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
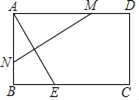
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,BC边上有一点E,BE=4,将纸片折叠,使A点与E点重合,折痕MN交AD于M点,则线段AM的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某个图形是按下面方法连接而成的:(0,0)→(2,0);(1,0)→(0,﹣1);(1,1)→(1,﹣2);(1,0)→(2,﹣1).
(1)请连接图案,它是一个什么汉字?
(2)作出这个图案关于y轴的轴对称图形,并写出新图案相应各端点的坐标,你得到一个什么汉字?
查看答案和解析>>
科目:初中数学 来源: 题型:
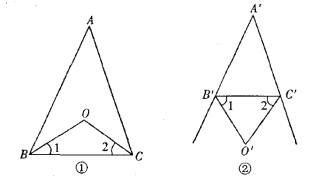
【题目】(1)如图①,在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;
(2)如图②,△A′B′C′的外角平分线相交于点O′,∠A′=40°,求∠B′O′C′的度数;
(3)上面(1)(2)两题中的∠BOC与∠B′O′C′ 有怎样的数量关系?若∠A=∠A′=n°,∠BOC与∠B′O′C′ 是否还具有这样的关系?这个结论你是怎样得到的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com