
【题目】如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
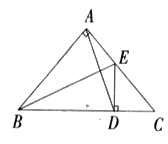
(1)请你写出图中所有的等腰三角形;
(2)请你判断AD与BE垂直吗?并说明理由.
(3)如果BC=10,求AB+AE的长.
【答案】(1)△ABC,△ABD,△ADE,△EDC(2)垂直,理由见解析(3)10.
【解析】
(1)根据等腰三角形的定义判断;
(2)由题意可知△ABE关于BE与△DBE对称,可得出BE⊥AD;
(3)根据(2),可知△ABE关于BE与△DBE对称,且△DEC为等腰直角三角形,可推出AB+AE=BD+DC=BC=10.
(1)△ABC等腰直角三角形,BE为角平分线;易证△ABE≌△DBE,即AB=BD,AE=DE,所以△ABD和△ADE均为等腰三角形;∠C=45°,ED⊥DC,△EDC也符合题意,综上所述符合题意的三角形为有△ABC,△ABD,△ADE,△EDC;
(2)AD与BE垂直.
证明:由BE为∠ABC的平分线,
知∠ABE=∠DBE,∠BAE=∠BDE=90°,AE=DE,
∴△ABE沿BE折叠,一定与△DBE重合.
∵A、D是对称点,
∴AD⊥BE;
(3)∵△ABD,△ADE,△EDC是等腰三角形
∴AB=BD,AE=DE=DC,
∴AB+AE=BD+DC=BC=10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某工厂需要在规定时间内生产1000个某种零件,该工厂按一定速度加工6天后,发现按此速度加工下去会延期4天完工,于是又抽调了一批工人投入这种零件的生产,使工作效率提高了![]() ,结果如期完成生产任务.
,结果如期完成生产任务.
(1)求该工厂前6天每天生产多少个这种零件;
(2)求规定时间是多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
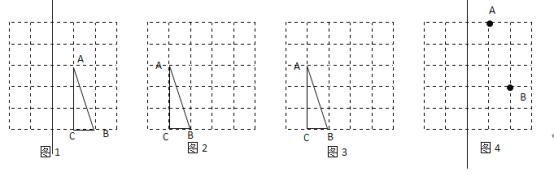
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点,
的小正方形构成的网格,每个小正方形的顶点叫做格点,![]() 的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ;
;
(2)如图![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如图![]() ,作
,作![]() 的中线
的中线![]() ;
;
(4)如图![]() ,在直线
,在直线![]() 上作出一条长度为
上作出一条长度为![]() 个单位长度的线段
个单位长度的线段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=![]() .
.
(1)最大的四位“言唯一数”是 ,最小的三位“言唯一数”是 ;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
查看答案和解析>>
科目:初中数学 来源: 题型:
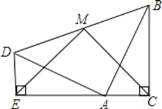
【题目】两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.

(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
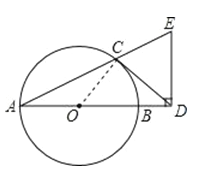
【题目】如图,AB 是⊙O 的直径,CD 与⊙O 相切于点 C,与 AB 的延长线交于点 D,DE⊥AD 且与AC 的延长线交于点 E.
(1)求证:DC=DE;
(2)若 AD=2ED,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了。有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() ,此时可以得到数字密码171920.
,此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个).
分解因式后可以形成哪些数字密码?(写出三个).
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为![]() ,求出一个由多项式
,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可).
分解因式后得到的密码(只需一个即可).
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为2434,求
时可以得到其中一个密码为2434,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com