
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.

(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
【答案】(1)AB=2;相等;(2)a=±![]() ;(3)
;(3)![]() ,∴
,∴![]() .
.
【解析】
试题(1)过点B作BN⊥x轴于N,由题意可知△AMB为等腰直角三角形,设出点B的坐标为(n,-n),根据二次函数得出n的值,然后得出AB的值;(2)根据抛物线的性质相同得出抛物线的完美三角形全等,从而得出点B的坐标,得出a的值;根据最大值得出mn-4m-1=0,根据抛物线的完美三角形的斜边长为n得出点B的坐标,然后代入抛物线求出m和n的值.
试题解析:(1)①过点B作BN⊥x轴于N,由题意可知△AMB为等腰直角三角形,AB∥x轴,
易证MN=BN,设B点坐标为(n,-n),代入抛物线![]() ,得
,得![]() ,
,
∴![]() ,
,![]() (舍去),∴抛物线
(舍去),∴抛物线![]() 的“完美三角形”的斜边
的“完美三角形”的斜边![]()
②相等;
(2)∵抛物线![]() 与抛物线
与抛物线![]() 的形状相同,
的形状相同,
∴抛物线![]() 与抛物线
与抛物线![]() 的“完美三角形”全等,
的“完美三角形”全等,
∵抛物线![]() 的“完美三角形”斜边的长为4,∴抛物线
的“完美三角形”斜边的长为4,∴抛物线![]() 的“完美三角形”斜边的长为4,
的“完美三角形”斜边的长为4,
∴B点坐标为(2,2)或(2,-2),∴![]() .
.
(3)∵![]() 的最大值为-1,∴
的最大值为-1,∴![]() ,
,
∴![]() ,∵抛物线
,∵抛物线![]() 的“完美三角形”斜边长为n,
的“完美三角形”斜边长为n,
∴抛物线![]() 的“完美三角形”斜边长为n,∴B点坐标为
的“完美三角形”斜边长为n,∴B点坐标为![]() ,
,
∴代入抛物线![]() ,得
,得![]() ,∴
,∴![]() (不合题意舍去),
(不合题意舍去),
∴![]() ,∴
,∴![]()


科目:初中数学 来源: 题型:
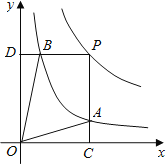
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
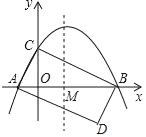
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2)
(1)求抛物线的表达式;
(2)抛物线的对称轴与x轴交于点M,点D与点C关于点M对称,试问在该抛物线的对称轴上是否存在点P,使△BMP与△ABD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
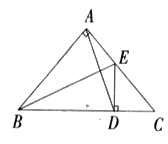
(1)请你写出图中所有的等腰三角形;
(2)请你判断AD与BE垂直吗?并说明理由.
(3)如果BC=10,求AB+AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是“五四”运动![]() 周年,为进一步弘扬“爱国、进步、民主、科学”的五四精神,引领广大团员青年坚定理想信念,某市团委、少先队共同举办纪念“五四运动
周年,为进一步弘扬“爱国、进步、民主、科学”的五四精神,引领广大团员青年坚定理想信念,某市团委、少先队共同举办纪念“五四运动![]() 周年”读书演讲比赛,甲同学代表学校参加演讲比赛,
周年”读书演讲比赛,甲同学代表学校参加演讲比赛,![]() 位评委给该同学的打分(单位:分)情况如下表:
位评委给该同学的打分(单位:分)情况如下表:
评委 | 评委1 | 评委2 | 评委3 | 评委4 | 评委5 | 评委6 | 评委7 |
打分 |
|
|
|
|
|
|
|
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
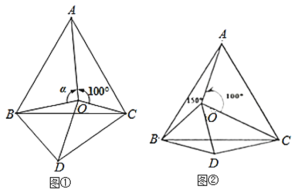
【题目】如图①,点![]() 是等边
是等边![]() 内一点,
内一点,![]() ,
,![]() .以
.以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时(如图②),试判断
时(如图②),试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)求当![]() 是多少度时,
是多少度时,![]() 是等腰三角形?(写出过程)
是等腰三角形?(写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
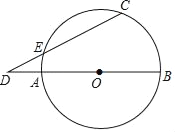
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,点D在BA的延长线上,CD与⊙O交于另一点E,DE=OB=2,∠D=20°,则弧BC的长度为( )
A. ![]() π B.
π B. ![]() π C.
π C. ![]() π D.
π D. ![]() π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com