
分析 (1)根据二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,也可以用配方法解决问题.
(2)求出抛物线与坐标轴的交点坐标,即可解决.
解答 解:(1)二次函数y=2x2+5x-3的对称轴x=-$\frac{b}{2a}$=-$\frac{5}{4}$,
∵$\frac{4ac-{b}^{2}}{4a}$=$\frac{-24-25}{8}$-$\frac{49}{8}$,
∴顶点坐标为(-$\frac{5}{4}$,-$\frac{49}{8}$).
(2)对于抛物线y=2x2+5x-3令x=0,得y=-3,所以抛物线与y轴交于点A(0,-3),
令y=0,得到2x2+5x-3=0,解得x=-3或$\frac{1}{2}$,
所以抛物线与x轴交于点B(-3,0)或C($\frac{1}{2}$,0),
∴抛物线与坐标轴交点坐标为顶点的几何图形△ABC的面积=$\frac{1}{2}$×$\frac{7}{2}$×3=$\frac{21}{4}$.
点评 本题考查抛物线与x轴的交点,二次函数的顶点坐标公式,对称轴等知识,解题的关键是记住抛物线的顶点坐标公式,对称轴公式,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:解答题
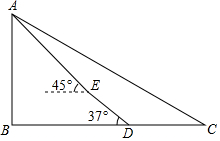 今年国庆节,小明与爸爸一起去省级风景名胜区彭祖山游览,小明想估算彭祖山AB的高度,如图,他在距山脚下400米的C点测得山顶的仰角为30°,来到山脚下D点,沿37°斜坡DE走400米到彭祖墓前,测得山顶的仰角为45°,请你帮助小明估算一下彭祖山的高度.(结果精确到1m)(参考数据:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414,sin37°=0.6,cos37°=0.8,tan37°=0.75,cot37°=1.33)
今年国庆节,小明与爸爸一起去省级风景名胜区彭祖山游览,小明想估算彭祖山AB的高度,如图,他在距山脚下400米的C点测得山顶的仰角为30°,来到山脚下D点,沿37°斜坡DE走400米到彭祖墓前,测得山顶的仰角为45°,请你帮助小明估算一下彭祖山的高度.(结果精确到1m)(参考数据:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414,sin37°=0.6,cos37°=0.8,tan37°=0.75,cot37°=1.33)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角坐标平面内,二次函数为y=a(x-1)2+4图象过点B(3,0).
在直角坐标平面内,二次函数为y=a(x-1)2+4图象过点B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
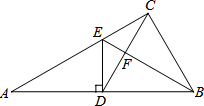 如图,D为直角△ABC的斜边AB上一点,DE⊥AB交AC于E,如果△AED沿DE翻折,A恰好与B重合,联结CD交BE于F,如果AC=8,tanA=$\frac{1}{2}$,那么CF:DF=6:5.
如图,D为直角△ABC的斜边AB上一点,DE⊥AB交AC于E,如果△AED沿DE翻折,A恰好与B重合,联结CD交BE于F,如果AC=8,tanA=$\frac{1}{2}$,那么CF:DF=6:5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com