
ЁОЬтФПЁПзлКЯгыЪЕМљЉЫФБпаЮа§зЊжаЕФЪ§бЇ
ЁАжЧЛлЁБЪ§бЇаЁзщдкПЮЭтЪ§бЇЛюЖЏжабаОПСЫвЛИіЮЪЬтЃЌЧыАяЫћУЧНтД№ЃЎ
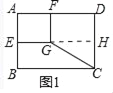
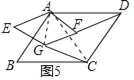
ШЮЮёвЛЃКШчЭМ1ЃЌдкОиаЮABCDжаЃЌAB=6ЃЌAD=8ЃЌEЃЌFЗжБ№ЮЊABЃЌADБпЕФжаЕуЃЌЫФБпаЮAEGFЮЊОиаЮЃЌСЌНгCGЃЎ
ЃЈ1ЃЉЧыжБНгаДГіCGЕФГЄЪЧ______ЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕБОиаЮAEGFШЦЕуAа§зЊЃЈБШШчЫГЪБеыа§зЊЃЉжСЕуGТфдкБпABЩЯЪБЃЌЧыМЦЫуDFгыCGЕФГЄЃЌЭЈЙ§МЦЫуЃЌЪдВТЯыDFгыCGжЎМфЕФЪ§СПЙиЯЕЃЎ
ЃЈ3ЃЉЕБОиаЮAEGFШЦЕуAа§зЊжСШчЭМ3ЕФЮЛжУЪБЃЌЃЈ2ЃЉжаDFгыCGжЎМфЕФЪ§СПЙиЯЕЪЧЗёЛЙГЩСЂЃПЧыЫЕУїРэгЩЃЎ
ШЮЮёЖўЃКЁАжЧЛлЁБЪ§бЇаЁзщЖдЭМаЮЕФа§зЊНјааСЫЭиеЙбаОПЃЌШчЭМ4ЃЌдкABCDжаЃЌЁЯB=60ЁуЃЌAB=6ЃЌAD=8ЃЌEЃЌFЗжБ№ЮЊABЃЌADБпЕФжаЕуЃЌЫФБпаЮAEGFЮЊЦНааЫФБпаЮЃЌСЌНгCGЃЎЁАжЧЛлЁБЪ§бЇаЁзщЗЂЯжDFгыCGШдШЛДцдкзХЬиЖЈЕФЪ§СПЙиЯЕЃЎ
ЃЈ4ЃЉШчЭМ5ЃЌЕБAEGFШЦЕуAа§зЊЃЈБШШчЫГЪБеыа§зЊЃЉЃЌЦфЫћЬѕМўВЛБфЪБЃЌЁАжЧЛлЁБЪ§бЇаЁзщЗЂЯжDFгыCGШдШЛДцдкзХетвЛЬиЖЈЕФЪ§СПЙиЯЕЃЎЧыФужБНгаДГіетИіЬиЖЈЕФЪ§СПЙиЯЕЃЎ





ЁОД№АИЁП5
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌгЩДЫEGНЛCDгкHЃЌдђЫФБпаЮFGHDЪЧОиаЮЃЎдкRtЁїCGHжаЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉШчЭМ2жаЃЌзїFPЁЭADгкPЃЎРћгУЙДЙЩЖЈРэЯрЫЦШ§НЧаЮЕФаджЪЃЌЗжБ№ЧѓГіCGЁЂDFМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉГЩСЂЃЎСЌНгAGЁЂACЃЎжЛвЊжЄУїЁїADFЁзЁїACGЃЌПЩЕУ![]() МДПЩНтОіЮЪЬтЃЛ
МДПЩНтОіЮЪЬтЃЛ
ЃЈ4ЃЉдкЭМ4жаЃЌЭЈЙ§МЦЫуМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉШчЭМ1жаЃЌгЩДЫEGНЛCDгкHЃЌдђЫФБпаЮFGHDЪЧОиаЮЃЎ
дкRtЁїCGHжаЃЌGH=DF=4ЃЌCH=DH=AE=3ЃЌ
ЁрCG=![]() =5ЃЎ
=5ЃЎ
ЙЪД№АИЮЊЃК5ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌзїFPЁЭADгкPЃЎ
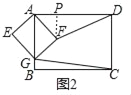
дкОиаЮAEGFжаЃЌЁпAE=3ЃЌEG=4ЃЌ
ЁрAG=5ЃЌBG=AB-AG=1ЃЌ
дкRtЁїCBGжаЃЌCG=![]() ЃЌ
ЃЌ
гЩЁїAPFЁзЁїAEGЃЌПЩЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAP=![]() ЃЌPF=
ЃЌPF=![]() ЃЌDP=ADЉAP=8Љ
ЃЌDP=ADЉAP=8Љ![]() ЃЌ
ЃЌ
дкRtЁїPDFжаЃЌDF=![]()
![]() ЃЌ
ЃЌ
ЁрDF=![]() CGЃЎ
CGЃЎ
ЃЈ3ЃЉГЩСЂЃЎРэгЩШчЯТЃКСЌНгAGЁЂACЃЎ
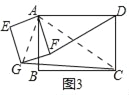
гЩа§зЊПЩжЊЃКЁЯDAF=ЁЯCAGЃЌ
гЩЙДЙЩЖЈРэПЩжЊЃКAC=![]() ЃЌAG=5ЃЌ
ЃЌAG=5ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЁїADFЁзЁїACGЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрDF=![]() CGЃЎ
CGЃЎ
ЃЈ4ЃЉШчЭМ4жаЃЌбгГЄEGНЛCDгкHЃЌзїCKЁЭGHгкKЃЎ
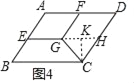
гЩЬтвтПЩжЊЫФБпаЮFGHDЪЧЦНааЫФБпаЮЃЌЫФБпаЮAEGFЪЧЦНааЫФБпаЮЃЌ
ЁрDF=GH=4ЃЌDH=FG=AE=3ЃЌCH=3ЃЌЁЯCHG=ЁЯD=60ЁуЃЌ
дкRtЁїCHKжаЃЌHK=![]() ЃЌCK=
ЃЌCK=![]() ЃЌGK=GHЉKH=
ЃЌGK=GHЉKH=![]() ЃЌ
ЃЌ
дкRtЁїCGKжаЃЌCG= ![]() ЃЌ
ЃЌ
ЁрCG=![]() DFЃЎ
DFЃЎ
дкЭМ5жаЃЌСЌНгAGЁЂACЃЎ
ЭЌЗЈПЩжЄЃКЁїACGЁзЁїADFЃЌПЩЕУЃК![]() =
=![]() ЃЌПЩЕУCG=
ЃЌПЩЕУCG=![]() DFЃЎ
DFЃЎ


 зДдЊЗЛШЋГЬЭЛЦЦЕМСЗВтЯЕСаД№АИ
зДдЊЗЛШЋГЬЭЛЦЦЕМСЗВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
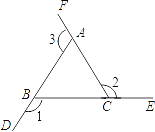
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=BCЃЌЁЯABC=90ЁуЃЌЕуFЮЊABбгГЄЯпЩЯвЛЕуЃЌЕуEдкBCЩЯЃЌBE=BFЃЌСЌНгAEЃЌEFКЭCFЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїCBFЃЛ
ЃЈ2ЃЉШєЁЯCAE=30ЁуЃЌЧѓЁЯEFCЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПБЛгўЮЊЁАжадЕквЛИпТЅЁБЕФжЃжнЛсеЙБіЙн(ЫзГЦЁАгёУзТЅЁБ)зјТфдкЗчОАШчЛЕФШчвтКўХЯЃЌЪЧРДжЃжнЙлЙтЕФгЮПЭСєгАЕФзюМбОАЕу.бЇЭъСЫШ§НЧКЏЪ§жЊЪЖКѓЃЌСѕУїКЭЭѕЛЊОіЖЈгУздМКбЇЕНЕФжЊЪЖВтСПЁАгёУзТЅЁБЕФИпЖШ.ШчЭМЃЌСѕУїдкЕуCДІВтЕУТЅЖЅBЕФбіНЧЮЊ45ЁуЃЌЭѕЛЊдкИпЬЈЩЯЕФDДІВтЕУТЅЖЅЕФбіНЧЮЊ40Ёу.ШєИпЬЈDEЕФИпЮЊ5УзЃЌЕуDЕНЕуCЕФЫЎЦНОрРыECЮЊ47.4УзЃЌAЃЌCЃЌEШ§ЕуЙВЯпЃЌЧѓЁАгёУзТЅЁБABЕФИпЖШ.(ВЮПМЪ§ОнЃКsin40ЁуЁж0.64ЃЌcos40ЁуЁж0.77ЃЌtan40ЁуЁж0.84ЃЌНсЙћБЃСєећЪ§)

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЮЛдЫЖЏдБдкОрРКЯТ4mДІЬјЦ№ЭЖРКЃЌЧђдЫааЕФТЗЯпЪЧХзЮяЯпЃЌЕБЧђдЫааЕФЫЎЦНОрРыЪЧ2.5mЪБЃЌДяЕНзюДѓИпЖШ3.5mЃЌШЛКѓзМШЗТфШыРКШІЃЎвбжЊРКШІжааФЕНЕиУцЕФОрРыЮЊ3.05mЃЎ
ЃЈ1ЃЉНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉИУдЫЖЏдБЩэИп1.8mЃЌдкетДЮЬјЭЖжаЃЌЧђдкЭЗЖЅЩЯ0.25mДІГіЪжЃЌ
ЮЪЃКЧђГіЪжЪБЃЌЫћОрРыЕиУцЕФИпЖШЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌАыдВOЕФжБОЖAB=10cmЃЌЯвAC=6cmЃЌНЋАыдВбизХЙ§ЕуAЕФжБЯпелЕўЃЌелЕўКѓЪЙЕУЯвACЧЁКУТфдкжБОЖABЩЯЃЌдђелКлADЕФГЄЮЊ_______cmЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌACЪЧABCDЕФЖдНЧЯпЃЌЕуEЪЧБпADЕФжаЕуЃЌСЌНгBEНЛACгкЕуFЃЌСЌНгCEЃЌDFЃЌШєЁЯBEC=ЁЯBAC=90ЁуЃЌдђsinЁЯDFEЕФжЕЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,ЕуPЪЧЕШБпШ§НЧаЮABCФквЛЕу,ЧвPA=3,PB=4, PC=5,ШєНЋЁїAPBШЦзХЕуBФцЪБеыа§зЊКѓЕУЕНЁїCQB,дђЁЯAPBЕФЖШЪ§______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2013ФъФГЦѓвЕАДВЭГјРЌЛјДІРэЗб25дЊ/ЖжЃЌНЈжўРЌЛјДІРэЗб16дЊ/ЖжБъзМЃЌЙВжЇИЖВЭГјКЭНЈжўРЌЛјДІРэЗб5200дЊЃЌДг2014ФъдЊдТЦ№ЃЌЪеЗбБъзМЩЯЕїЮЊЃКВЭГјРЌЛјДІРэЗб100дЊ/ЖжЃЌНЈжўРЌЛјДІРэЗб30дЊ/ЖжЃЌШєИУЦѓвЕ2014ФъДІРэЕФетСНжжРЌЛјЪ§СПгы2013ФъЯрБШУЛгаБфЛЏЃЌОЭвЊЖржЇИЖРЌЛјДІРэЗб8800дЊЃЌ
ЃЈ1ЃЉИУЦѓвЕ2013ФъДІРэЕФВЭГјРЌЛјКЭНЈжўРЌЛјИїЖрЩйЖжЃП
ЃЈ2ЃЉИУЦѓвЕМЦЛЎ2014ФъНЋЩЯЪіСНжжРЌЛјДІРэСПМѕЩйЕН240ЖжЃЌЧвНЈжўРЌЛјДІРэЗбВЛГЌЙ§ВЭГјРЌЛјДІРэСПЕФ3БЖЃЌдђ2014ФъИУЦѓвЕзюЩйашвЊжЇИЖетСНжжРЌЛјДІРэЗбЙВЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЩфЯпADЃЌBEЃЌCFЙЙГЩЁЯ1ЃЌЁЯ2ЃЌЁЯ3ЃЌдђЁЯ1+ЁЯ2+ЁЯ3=ЃЈ ЃЉ
A. 180Ёу B. 360Ёу C. 540Ёу D. ЮоЗЈШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com