练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．圆的两条平行弦的长分别为6、8，若圆的半径为5，则这两条平行弦之间的距离为7，1．

    分析 这两条平行弦可能位于圆心的同侧，也可能位于圆心的两侧，应分两种情况进行讨论，在同侧时，这两条平行弦之间的距离是两弦弦心距的差，在两侧时，这两条平行弦之间的距离是两弦弦心距的和．

    解答 解：在直角△OAC中，AC=$\frac{1}{2}$AB=3，
    OC=$\sqrt{O{A}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
    同理，EF的弦心距是3，
    当两条平行线在圆心的两侧时：两条平行弦之间的距离是4+3=7；
    当两条平行线在圆心的同侧时：两条平行弦之间的距离是4-3=1．
    故答案为：7或1．

    点评 本题考查了垂径定理的应用，利用垂径定理可以把求弦长或圆心角或弦心距的问题转化为解直角三角形的问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．计算：$\frac{\sqrt{15}}{\sqrt{6}}$×（-5$\sqrt{2\frac{2}{7}}$）÷2$\sqrt{28}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知函数y=（m2-4）x${\;}^{{m}^{2}-m-4}$+（m-3）x+2是二次函数，求它的解析式，并求出该二次函数的最大值或最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

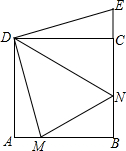    13．如图，在正方形ABCD中，AB=4，∠MDN=45°，点M，N分别在AB，BC边上，延长BC至E，使CE=AM，连接DE．
    （1）求证：DM=DE；
    （2）猜想MN，AM，CN之间有什么数量关系，并进行证明；
    （3）设AM=t，若△MDN为等腰三角形，请直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知A=$\frac{1}{5}$x3-3x2+$\frac{2}{3}$，B=$\frac{1}{10}$x3-$\frac{3}{5}$x2-$\frac{1}{2}$x，且x=-$\frac{2}{3}$，求A-2B的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）$\sqrt{\frac{16}{25}}$-$\root{3}{8}$+$\sqrt{0.01}$-（-3）2×$\root{3}{2\frac{10}{27}}$；
    （2）（-3ab2）3•（a2b-ab-1）；
    （3）（m-3）（m2+3m+9）；
    （4）（3x-2y）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．先化简，再求值：2x2y-[2x2z-（xy+x2z-2x2y）]，其中 x，y，z是你喜欢的数值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．解方程：
    （1）x2-3x-2=0     
    （2）（x-3）2=4x（x-3）
    （3）$\frac{x}{x-2}$=$\frac{3（x-2）}{x}$+2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

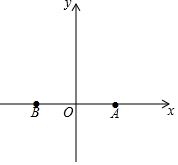    15．如图，在平面直角坐标系中，点A的坐标为（2，0），点A关于y轴的对称点为点B．
    （1）求点B的坐标；
    （2）若以AB为一边向上作一个等边三角形ABC，求点C的坐标；
    （3）求（2）中的三角形ABC的周长和面积．

    查看答案和解析>>

    同步练习册答案