
【题目】如图,AB是⊙O的直径,直线l与⊙O相切于点C,AE⊥l交直线l于点E、交⊙O于点F,BD⊥l交直线l于点D.
(1)求证:△AEC∽△CDB;
(2)求证:AE+EF=AB;
(3)若AC=8cm,BC=6cm,点P从点A出发沿线段AB向点B以2cm/s的速度运动,点Q从点B出发沿线段BC向点C以1cm/s的速度运动,两点同时出发,当点P运动到点B时,两点都停止运动.设运动时间为t秒,求当t为何值时,△BPQ为等腰三角形?

【答案】(1)证明见解析;(2)证明见解析;(3)当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时,△BPQ为等腰三角形.
时,△BPQ为等腰三角形.
【解析】试题分析:(1)、根据直角得出∠ACB=90°,即∠BCD+∠ACE=90°,根据AE⊥DE,BD⊥DE得出∠BCD=∠EAC,从而说明三角形相似;(2)、连接BF、OC根据DE为切线得出OC⊥DE,根据AE⊥DE,BD⊥DE得到OC∥BD∥AE,根据O为中点,得出OC为梯形的中位线,得到OC=![]() ,根据AB为直径得出∠BFE=90°,然后说明BDEF为矩形,得出BD=FE,即AE+EF=AE+BD,得到OC=
,根据AB为直径得出∠BFE=90°,然后说明BDEF为矩形,得出BD=FE,即AE+EF=AE+BD,得到OC=![]() ,从而说明结论;(3)、首先根据题意求出AB和BP的长度,根据BP=BQ,BP=PQ,BQ=PQ三种情况求出t的值.
,从而说明结论;(3)、首先根据题意求出AB和BP的长度,根据BP=BQ,BP=PQ,BQ=PQ三种情况求出t的值.
试题解析:(1)、∵AB是⊙O的直径 ∴∠ACB=90° ∴∠BCD+∠ACE=180°-∠ACB=90°
∵AE⊥DE,BD⊥DE ∴∠AEC=∠BDC=90° ∴∠ACE +∠EAC=90° ∴∠BCD =∠EAC ∴△AEC∽△CDB
(2)、连结BF、OC ∵DE切⊙O于点C ∴OC⊥DE
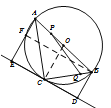
又∵AE⊥DE,BD⊥DE ∴OC∥BD∥AE又∵O是AB的中点 ∴OC是梯形ABDE的中位线
∴OC=![]() ∵AB是⊙O的直径 ∴∠AFB=90° ∴∠BFE=90°
∵AB是⊙O的直径 ∴∠AFB=90° ∴∠BFE=90°
又∵∠AED=∠BDE=90° ∴四边形BDEF是矩形
∴BD=FE ∴AE+EF=AE+BD ∴OC=![]() ∵OC=
∵OC= ![]() ∴AE+EF=AB
∴AE+EF=AB
(3)、由题意可知:AP=2t,BQ=t,0<t≤5 ∵∠ACB=90° ,AC="8,BC=6" ∴AB=![]() ∴BP=10-2t
∴BP=10-2t
当BP=BQ时 10-2t=t t=![]()
②当PB=PQ时,过点P作PG⊥BC于点G ∵PB=PQ,PG⊥BC
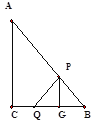
∴BG= ![]() =
= ![]() ,∠PGB=90°∴∠ACB=∠PGB =90° 又∵∠PBG=∠ABC ∴△BPG∽△BAC
,∠PGB=90°∴∠ACB=∠PGB =90° 又∵∠PBG=∠ABC ∴△BPG∽△BAC
∴![]() ∴
∴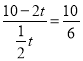
③当BQ=PQ时,过点Q作QH⊥AB于点H同理可求得:BH= ![]() =
= ![]() ,
,
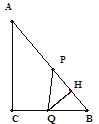
△QHB∽△ACB ∴![]() ∴
∴![]() ∴t=
∴t=![]()
综上所述,当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时,△BPQ为等腰三角形.
时,△BPQ为等腰三角形.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
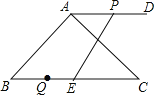
【题目】如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
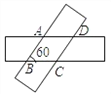
【题目】如图,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于__________cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 | …… | -4 | -2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据,科学家推测出植物每天高度增长量![]() 是温度
是温度![]() 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度![]() 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com