
如图,已知抛物线y=ax2+bx﹣4与x轴交于A(﹣2,0),B(8,0)两点,与y轴交于点C,连接BC,以BC为一边,作菱形BDEC,使其对角线在坐标轴上,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求抛物线的解析式;
(2)将抛物线向上平移n个单位,使其顶点在菱形BDEC内(不含菱形的边),求n的取值范围;
(3)当点P在线段OB上运动时,直线l交BD于点M.试探究m为何值时,四边形CQMD是平行四边形,并说明理由.
(1)y= x2﹣
x2﹣ x﹣4;(2)
x﹣4;(2) ;(3)m=4时,四边形CQMD是平行四边形,理由详见解析.
;(3)m=4时,四边形CQMD是平行四边形,理由详见解析.
解析试题分析:(1)由待定系数法即可求得.
(2)先求得直线BC的解析式和抛物线的顶点坐标G(3,﹣ ),然后把x=3代入直线BC的解析式即可求得F的坐标,进而求得E的坐标即可求得n的取值.
),然后把x=3代入直线BC的解析式即可求得F的坐标,进而求得E的坐标即可求得n的取值.
(3)由菱形的对称性可知,点D的坐标,根据待定系数法可求直线BD的解析式,根据平行四边形的性质可得关于m的方程,求得m的值;再根据平行四边形的判定可得四边形CQBM的形状;
试题解析:(1)∵抛物线y=ax2+bx﹣4与x轴交于A(﹣2,0),B(8,0)两点,
∴ 解得
解得
∴抛物线的解析式为:y= x2﹣
x2﹣ x﹣4;
x﹣4;
(2)设抛物线的顶点为G,过G点作x轴的垂线交BD于E,交BC于F,
由抛物线的解析式y= x2﹣
x2﹣ x﹣4可知C(0,﹣4)
x﹣4可知C(0,﹣4)
设直线BC的解析式为y=k1x+b1,
∵B(8,0),C(0,﹣4),则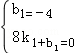 ,
,
解得k1= ,b1=﹣4.
,b1=﹣4.
故直线BC的解析式为y= x﹣4.
x﹣4.
∵y= x2﹣
x2﹣ x﹣4=
x﹣4= (x﹣3)2﹣
(x﹣3)2﹣ ,
,
∴抛物线的顶点G的坐标(3,﹣ ),
),
当x=3时,y=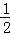 x﹣4=﹣
x﹣4=﹣ ,
,
∴F(3,﹣ ),
),
由菱形的对称性可知,点E的坐标为(3, ).
).
∵GF=﹣ ﹣(﹣
﹣(﹣ )=
)= ,GE=
,GE= ﹣(﹣
﹣(﹣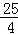 )=
)= ,
,
∴ <n<
<n< .
.
(3)∵C(0,﹣4)
∴由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则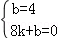 ,
,
解得k=﹣ ,b=4.
,b=4.
∴直线BD的解析式为y=﹣ x+4.
x+4.
∵l⊥x轴,
∴点M的坐标为(m,﹣ m+4),点Q的坐标为(m,
m+4),点Q的坐标为(m, m2﹣
m2﹣ m﹣4).
m﹣4).
如图,当MQ=DC时,四边形CQMD是平行四边形,
∴(﹣ m+4)﹣(
m+4)﹣(  m2﹣
m2﹣ m﹣4)=4﹣(﹣4).
m﹣4)=4﹣(﹣4).
化简得:m2﹣4m=0,
解得m1=0(不合题意舍去),m2=4.
∴当m=4时,四边形CQMD是平行四边形.

考点:1.待定系数法求函数解析式;2.平行四边形判定


科目:初中数学 来源: 题型:填空题
(2013年四川绵阳4分)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:
①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n< ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是 (写出你认为正确的所有结论序号).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知 球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?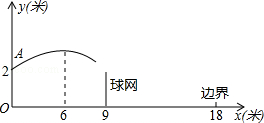
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
(1)当t为何值时,点A′与点C重合;
(2)用含t的代数式表示QF的长;
(3)求S与t的函数关系式;
(4)请直接写出当射线PQ将?A′PBE分成的两部分图形的面积之比是1:3时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“丹棱冻粑”是眉山著名特色小吃,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一次函数y=x–3的图象与 轴,
轴, 轴分别交于点
轴分别交于点 .一个二次函数y=x2+bx+c的图象经过点
.一个二次函数y=x2+bx+c的图象经过点 .
.
(1)求点 的坐标,并画出一次函数y=x–3的图象;
的坐标,并画出一次函数y=x–3的图象;
(2)求二次函数的解析式并求其图像顶点C的坐标.
(3)求 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:矩形ABCD中,M为BC边上一点, AB=BM=10,MC=14,如图1,正方形EFGH的顶点E和点B重合,点F、G、H分别在边AB、AM、BC上.如图2,P为对角线AC上一动点,正方形EFGH从图1的位置出发,以每秒1个单位的速度沿BC向点C匀速移动;同时,点P从C点出发,以每秒1个单位的速度沿CA向点A匀速移动.当点F到达线段AC上时,正方形EFGH和点P同时停止运动.设运动时间为t秒,解答下列问题:
(1)在整个运动过程中,当点F落在线段AM上和点G落在线段AC上时,分别求出对应t的值;
(2)在整个运动过程中,设正方形 与
与 重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
(3)在整个运动过程中,是否存在点P,使 是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
如图所示,已知平面直角坐标系xOy,抛物线过点A(4,0)、B(1,3)
【小题1】求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
【小题2】记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com