如图所示，已知平面直角坐标系xOy，抛物线过点A(4,0)、B(1,3)
【小题1】求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；
【小题2】记该抛物线的对称轴为直线l，设抛物线上的点P(m,n)在第四象限，点P关于直线l的对称点为E，点E关于y轴的对称点为F，若四边形OAPF的面积为20，求m、n的值.
考前必练系列答案科目：初中数学 来源： 题型：填空题
如图，抛物线
与y轴相交于点A，与过点A平行于x轴的直线相交于点B（点B在第一象限）．抛物线的顶点C在直线OB上，对称轴与x轴相交于点D．平移抛物线，使其经过点A、D，则平移后的抛物线的解析式为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：填空题
2013年5月26日，中国羽毛球队蝉联苏迪曼杯团体赛冠军，成就了首个五连冠霸业．比赛中羽毛球的某次运动路线可以看作是一条抛物线（如图）．若不考虑外力因素，羽毛球行进高度y（米）与水平距离x（米）之间满足关系
，则羽毛球飞出的水平距离为 米．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
用长为32米的篱笆围一个矩形养鸡场，设围成的矩形一边长为x米，面积为y平方米．
（1）求y关于x的函数关系式；
（2）当x为何值时，围成的养鸡场面积为60平方米？
（3）能否围成面积为70平方米的养鸡场？如果能，请求出其边长；如果不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，已知抛物线y=ax2+bx﹣4与x轴交于A（﹣2，0），B（8，0）两点，与y轴交于点C，连接BC，以BC为一边，作菱形BDEC，使其对角线在坐标轴上，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．
（1）求抛物线的解析式；
（2）将抛物线向上平移n个单位，使其顶点在菱形BDEC内（不含菱形的边），求n的取值范围；
（3）当点P在线段OB上运动时，直线l交BD于点M．试探究m为何值时，四边形CQMD是平行四边形，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，在直角坐标平面内，直线
与
轴和
轴分别交于A、B两点，二次函数
的图象经过点A、B，且顶点为C．
（1）求这个二次函数的解析式；
（2）求
的值；
（3）若P是这个二次函数图象上位于轴下方的一点，且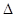
ABP的面积为10，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图1，边长为4的正方形ABCD中，点E在AB边上（不与点A，B重合），点F在BC边上（不与点B，C重合）．
第一次操作：将线段EF绕点F顺时针旋转，当点E落在正方形上时，记为点G；
第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；
依次操作下去…
（1）图2中的△EFD是经过两次操作后得到的，其形状为 ，求此时线段EF的长；
（2）若经过三次操作可得到四边形EFGH．
①请判断四边形EFGH的形状为 ，此时AE与BF的数量关系是 ；
②以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x的函数关系式及面积y的取值范围；
（3）若经过多次操作可得到首尾顺次相接的多边形，其最大边数是多少？它可能是正多边形吗？如果是，请直接写出其边长；如果不是，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的图象如图所示，则下列结论中：①
；②
；③
；④
．正确的是 ．