
��ͼ����Rt��ABC�У���ACB=90�㣬AC=8cm��AB=10cm����P�ӵ�A��������5cm/s���ٶȴӵ�A�˶����յ�B��ͬʱ����Q�ӵ�C��������3cm/s���ٶȴӵ�C�˶����յ�B������PQ������P��PD��AC��AC�ڵ�D������APD��PD���۵õ���A��PD����A��P��PBΪ�ڱ���?A��PBE��A��E������BC�ڵ�F��������PQ�ڵ�G����?A��PBE���ı���PDCQ�ص�����ͼ�ε����ΪScm2����P���˶�ʱ��Ϊts��
��1����tΪ��ֵʱ����A�����C�غϣ�
��2���ú�t�Ĵ���ʽ��ʾQF�ij���
��3����S��t�ĺ�����ϵʽ��
��4����ֱ��д��������PQ��?A��PBE�ֳɵ�������ͼ�ε����֮����1��3ʱt��ֵ��
��1��t=1��2����0��t��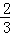 ʱ��QF=6��9t����
ʱ��QF=6��9t����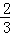 ��t��2ʱ��QF=9t��6��
��t��2ʱ��QF=9t��6��
��0��t��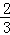 ʱ��S=12t2����
ʱ��S=12t2����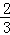 ��t��1ʱ��S=��42t2+72t��24����1��t��2ʱ��S=6t2��24t+24��
��t��1ʱ��S=��42t2+72t��24����1��t��2ʱ��S=6t2��24t+24��
t��ֵΪ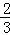 ���
���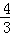 �룮
�룮
���������������1����֤��ADP�ס�ACB���Ӷ��ɵ�AD=4t�����۵��ɵ�AA��=2AD=8t���ɵ�A�����C�غϿɵ�8t=8���Ӷ��������t��ֵ��
��2�����ݵ�F��λ�ò�ͬ���ɷֵ�F��BQ�ϣ���������B������CQ�ϣ���������Q������BC���ӳ�������������������ۣ��Ϳɽ�����⣮
��3�����ݵ�F��λ�ò�ͬ���ɷֵ�F��BQ�ϣ���������B������CQ�ϣ���������Q������BC���ӳ�������������������ۣ��Ϳɽ�����⣮
��4���ɷ֢�S��A��PG��S�ı���PBEG=1��3����ͼ7����S��BPN��S�ı���PNEA��=1��3����ͼ8����������������ۣ��Ϳɽ�����⣮
�����������1����ͼ1��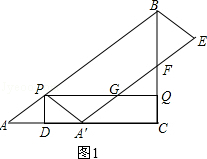
����ɵã�PA��=PA=5t��CQ=3t��AD=A��D��
�ߡ�ACB=90�㣬AC=8��AB=10����BC=6��
�ߡ�ADP=��ACB=90�㣬
��PD��BC��
���ADP�ס�ACB��
��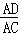 =
= =
=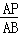 ��
��
��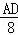 =
=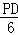 =
=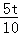 ��
��
��AD=4t��PD=3t��
��AA��=2AD=8t��
����A�����C�غ�ʱ��AA��=AC��
��8t=8��
��t=1��
��2���ٵ���F���߶�BQ�ϣ���������B��ʱ����ͼ1��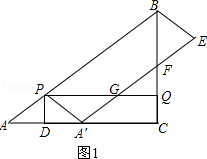
����CQ��CF��CB��
���ı���A��PBE��ƽ���ı��Σ�
��A��E��BP��
���CA��F�ס�CAB��
��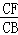 =
=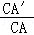 ��
��
��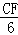 =
=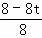 ��
��
��CF=6��6t��
��3t��6��6t��6��
��0��t��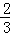 ��
��
��ʱQF=CF��CQ=6��6t��3t=6��9t��
�ڵ���F���߶�CQ�ϣ���������Q��ʱ����ͼ2��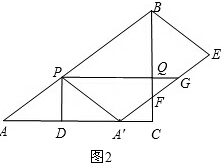
����0��CF��CQ��
��CF=6��6t��CQ=3t��
��0��6��6t��3t��
��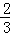 ��t��1��
��t��1��
��ʱQF=CQ��CF=3t����6��6t��=9t��6��
�۵���F���߶�BC���ӳ�����ʱ����ͼ3��
����AA�䣾AC����AP��AB��
��8t��8����5t��10��
��1��t��2��
ͬ���ɵã�CF=6t��6��
��ʱQF=QC+CF=3t+6t��6=9t��6��
������������0��t��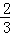 ʱ��QF=6��9t����
ʱ��QF=6��9t����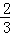 ��t��2ʱ��QF=9t��6��
��t��2ʱ��QF=9t��6��
��3���ٵ�0��t��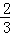 ʱ��
ʱ��
���� A����A��M��PG������ΪM����ͼ4��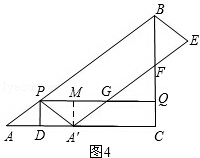
����A��M=CQ=3t��
��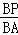 =
=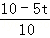 =
=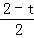 ��
�� =
=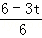 =
=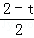 ��
��
��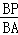 =
=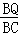 ��
��
�ߡ�PBQ=��ABC��
���BPQ�ס�BAC��
���BQP=��BCA��
��PQ��AC��
��AP��A��G��
���ı���APGA����ƽ���ı��Σ�
��PG=AA��=8t��
��S=S��A��PG=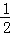 PG•A��M
PG•A��M
=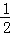 ��8t��3t=12t2��
��8t��3t=12t2��
�ڵ�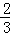 ��t��1ʱ��
��t��1ʱ��
���� A����A��M��PG������ΪM����ͼ5��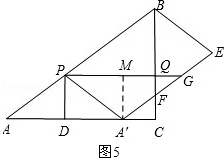
����A��M=QC=3t��PQ=DC=8��4t��PG=AA��=8t��QG=PG��PQ=12t��8��QF=9t��6����
��S=S��A��PG��S��GQF
=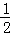 PG•A��M��
PG•A��M��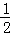 QG•QF
QG•QF
=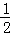 ��8t��3t��
��8t��3t��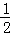 ����12t��8������9t��6��
����12t��8������9t��6��
=��42t2+72t��24��
�۵�1��t��2ʱ����ͼ6��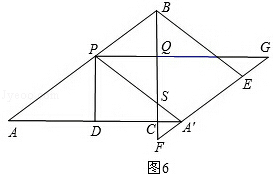
��PQ��AC��PA=PA��
���BPQ=��PAA�䣬��QPA��=��PA��A����PAA��=��PA��A��
���BPQ=��QPA�䣮
�ߡ�PQB=��PQS=90�㣬
���PBQ=��PSQ��
��PB=PS��
��BQ=SQ��
��SQ=6��3t��
��S=S��PQS= PQ•QS=
PQ•QS= ����8��4t������6��3t��=6t2��24t+24��
����8��4t������6��3t��=6t2��24t+24��
������������0��t��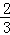 ʱ��S=12t2����
ʱ��S=12t2����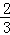 ��t��1ʱ��S=��42t2+72t��24
��t��1ʱ��S=��42t2+72t��24


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
2013��5��26�գ��й���ë��Ӳ����յ������������ھ����ɾ����������ڰ�ҵ����������ë���ij���˶�·�߿��Կ�����һ�������ߣ���ͼ�������������������أ���ë���н��߶�y���ף���ˮƽ����x���ף�֮�������ϵ ������ë��ɳ���ˮƽ����Ϊ�� ���ף�
������ë��ɳ���ˮƽ����Ϊ�� ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�ó�Ϊ32�����Χһ����������������Χ�ɵľ���һ�߳�Ϊx�ף����Ϊyƽ���ף�
��1����y����x�ĺ�����ϵʽ��
��2����xΪ��ֵʱ��Χ�ɵ����������Ϊ60ƽ���ף�
��3���ܷ�Χ�����Ϊ70ƽ����������������ܣ��������߳���������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������y=ax2+bx��4��x�ύ��A����2��0����B��8��0�����㣬��y�ύ�ڵ�C������BC����BCΪһ�ߣ�������BDEC��ʹ��Խ������������ϣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��1���������ߵĽ���ʽ��
��2��������������ƽ��n����λ��ʹ�䶥��������BDEC�ڣ��������εıߣ�����n��ȡֵ��Χ��
��3������P���߶�OB���˶�ʱ��ֱ��l��BD�ڵ�M����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪������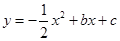 ͼ��A��-1��0����B��4��0�����㣮
ͼ��A��-1��0����B��4��0�����㣮
��1���������ߵĽ���ʽ��
��2����C��m��m-1������������λ�ڵ�һ�����ڵĵ㣬D���߶�AB�ϵ�һ�����㣨����A��B�غϣ�������D�ֱ���DE��BC��AC��E��DF��AC��BC��F��
����֤���ı���DECF�Ǿ��Σ�
������EF���߶�EF�ij��Ƿ������Сֵ�������ڣ����EF����Сֵ���������ڣ���˵�����ɣ�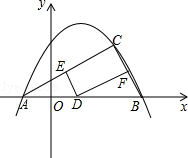
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ֱ������ƽ���ڣ�ֱ�� ��
�� ���
��� ��ֱ���A��B���㣬���κ���
��ֱ���A��B���㣬���κ��� ��ͼ����A��B���Ҷ���ΪC��
��ͼ����A��B���Ҷ���ΪC��
��1����������κ����Ľ���ʽ��
��2���� ��ֵ��
��ֵ��
��3����P��������κ���ͼ����λ�� ���·���һ�㣬��
���·���һ�㣬��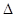 ABP�����Ϊ10�����P�����꣮
ABP�����Ϊ10�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�������ߣ�y��ax2��bx��4��x�ύ�ڵ�A(��2��0)��B(4��0)����y�ύ�ڵ�C��
(1)�������ߵĽ���ʽ��
(2)T�������߶Գ����ϵ�һ�㣬�ҡ�ACT����ACΪ�ĵ��������Σ����T�����ꣻ
(3)��M��Q�ֱ�ӵ�A��B��ÿ��1����λ���ȵ��ٶ���x��ͬʱ����������У�����Mԭ��ʱ����Q���̵�ͷ����ÿ�����λ���ȵ��ٶ����B�����ƶ�������M���������ߵĶԳ���ʱ������ֹͣ�˶�������M��ֱ��l���ᣬ��AC��BC�ڵ�P�����M���˶�ʱ��t(��)���APQ�����S�ĺ�����ϵʽ�������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ֱ�� ��x�ᣬy��ֱ��ཻ�ڵ�B����C������B��C�����������
��x�ᣬy��ֱ��ཻ�ڵ�B����C������B��C����������� ��x�����һ����ΪA������ΪP���ҶԳ�����ֱ��
��x�����һ����ΪA������ΪP���ҶԳ�����ֱ�� ��
��
��1����A������꼰�������ߵĺ�������ʽ��
��2�����∆PBC�������
��3�������ڶԳ��� �Ҳ�����������Ƿ���ڵ�Q��ʹ���Ե�A��B��C��Q��Χ�ɵ��ı��������∆PBC�������
�Ҳ�����������Ƿ���ڵ�Q��ʹ���Ե�A��B��C��Q��Χ�ɵ��ı��������∆PBC������� �������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com