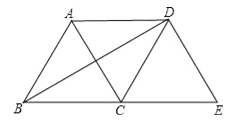
【题目】如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：
①AC=AD；②BD⊥AC；③四边形ACED是菱形．
其中正确的个数是（ ）
A．0 B．1 C．2 D．3
科目：初中数学 来源： 题型：
【题目】如图在△AFD和△CEB中,点A、E、F、C在同一条直线上.有下面四个论断：
(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC.
请用其中三个作为条件,余下一个作为结论,进行证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学问题：计算
（其中m，n都是正整数，且m≥2，n≥1）．
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算
．
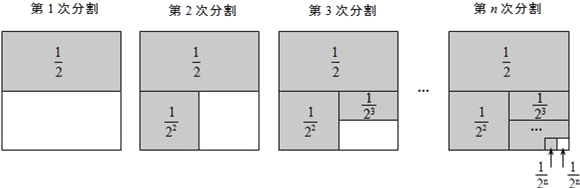
第1次分割，把正方形的面积二等分，其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为
，最后空白部分的面积是
．
根据第n次分割图可得等式： 
=1﹣
．
探究二：计算
．
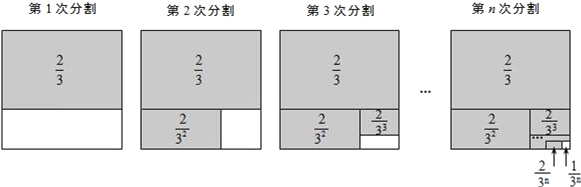
第1次分割，把正方形的面积三等分，其中阴影部分的面积为
；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为
；
第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为
，最后空白部分的面积是
．
根据第n次分割图可得等式： 
=1﹣
，
两边同除以2，得
=
.
探究三：计算
．
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算
．
（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式： ，
所以， 
= ．
拓广应用：计算
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小亮家与姥姥家相距24km，小亮8：00从家出发，骑自行车去姥姥家．妈妈8：30从家出发，乘车沿相同路线去姥姥家．在同一直角坐标系中，小亮和妈妈的行进路程S（km）与北京时间t（时）的函数图象如图所示．根据图象得到小亮结论，其中错误的是（ ）
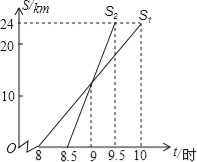
A. 小亮骑自行车的平均速度是12km/h
B. 妈妈比小亮提前0.5小时到达姥姥家
C. 妈妈在距家12km处追上小亮
D. 9：30妈妈追上小亮
查看答案和解析>>
科目：初中数学 来源： 题型：
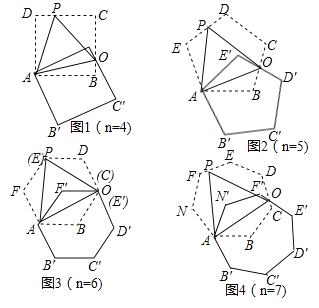
【题目】如图，将正n边形绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为“叠弦角”，△AOP为“叠弦三角形”．
【探究证明】
（1）请在图1和图2中选择其中一个证明：“叠弦三角形”（△AOP）是等边三角形；
（2）如图2，求证：∠OAB=∠OAE′．
【归纳猜想】
（3）图1、图2中的“叠弦角”的度数分别为 ， ；
（4）图n中，“叠弦三角形” 等边三角形（填“是”或“不是”）
（5）图n中，“叠弦角”的度数为 （用含n的式子表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
