
【题目】已知:在平面直角坐标系中,抛物线![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.

(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
【答案】(1)y=﹣![]() (x+2)2+4,顶点D的坐标为(﹣2,4);(2)S=﹣2t+12,t=4时,S有最小值,最小值4;(3) 点P的坐标为(0,2).
(x+2)2+4,顶点D的坐标为(﹣2,4);(2)S=﹣2t+12,t=4时,S有最小值,最小值4;(3) 点P的坐标为(0,2).
【解析】(1)对称轴为x=﹣ =﹣2,
=﹣2,
解得b=﹣1,
所以,抛物线的解析式为y=﹣![]() x2﹣x+3,
x2﹣x+3,
∵y=﹣![]() x2﹣x+3=﹣
x2﹣x+3=﹣![]() (x+2)2+4,
(x+2)2+4,
∴顶点D的坐标为(﹣2,4);
(2)令y=0,则﹣![]() x2﹣x+3=0,
x2﹣x+3=0,
整理得,x2+4x﹣12=0,
解得x1=﹣6,x2=2,
∴点A(﹣6,0),B(2,0),
如图1,过点D作DE⊥y轴于E,
∵0≤t≤4,
∴△PAD的面积为S=S梯形AOED﹣S△AOP﹣S△PDE,
=![]() ×(2+6)×4﹣
×(2+6)×4﹣![]() ×6t﹣
×6t﹣![]() ×2×(4﹣t),
×2×(4﹣t),
=﹣2t+12,
∵k=﹣2<0,
∴S随t的增大而减小,
∴t=4时,S有最小值,最小值为﹣2×4+12=4;
(3)如图2,过点D作DF⊥x轴于F,
∵A(﹣6,0),D(﹣2,4),
∴AF=﹣2﹣(﹣6)=4,
∴AF=DF,
∴△ADF是等腰直角三角形,
∴∠ADF=45°,
由二次函数对称性,∠BDF=∠ADF=45°,
∴∠PDA=90°时点P为BD与y轴的交点,
∵OF=OB=2,
∴PO为△BDF的中位线,
∴OP=![]() DF=2,
DF=2,
∴点P的坐标为(0,2),
由勾股定理得,DP=![]() =2
=2![]() ,
,
AD=![]() AF=4
AF=4![]() ,
,
∴![]() =
=![]() =2,
=2,
令x=0,则y=3,
∴点C的坐标为(0,3),OC=3,
∴![]() =
=![]() =2,
=2,
∴![]() =
=![]() ,
,
又∵∠PDA=90°,∠COA=90°,
∴Rt△ADP∽Rt△AOC.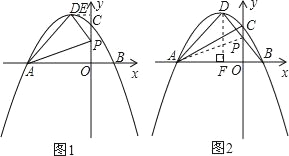


科目:初中数学 来源: 题型:
【题目】为了了解青少年形体情况,现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对测评数据作了适当处理(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
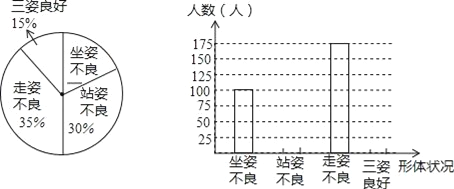
(1)请将两幅统计图补充完整;
(2)请问这次被抽查形体测评的学生一共是多少人?
(3)如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0),点P是直线AB上的一个动点,记点P关于y轴对称的点为P′.
(1)当b=3时(如图1),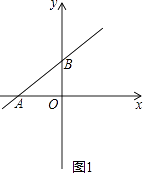
①求直线AB的函数表达式.
(2)②在x轴上找一点Q(点O除外),使△APQ与△AOB全等,直接写出点Q的所有坐标
(3)若点P在第一象限(如图2),设点P的横坐标为a,作PC⊥x轴于点C,连结AP′,CP′.当△ACP′是以点P′为直角顶点的等腰直角三角形时,求出a,b的值.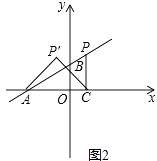
(4)当线段OP′恰好被直线AB垂直平分时(如图3),直接写出b= . 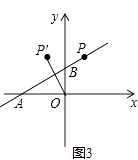
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每件进价为10元,调查表明:在某段时间内若以每件x元(10≤x≤20且x为整数)出售,可卖出(20﹣x)件,若使利润最大,则每件商品的售价应为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求:
(1)∠FED的度数;
(2)∠FEG的度数;
(3)∠1和∠2的度数.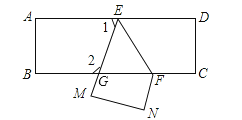
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com