
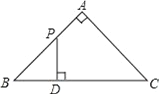
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. 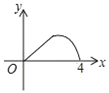 B.
B. 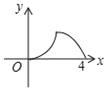 C.
C. 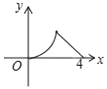 D.
D. 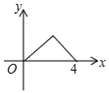
【答案】B
【解析】过A点作AH⊥BC于H,利用等腰直角三角形的性质得到∠B=∠C=45°,BH=CH=AH=![]() BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y=
BC=2,分类讨论:当0≤x≤2时,如图1,易得PD=BD=x,根据三角形面积公式得到y=![]() x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣
x2;当2<x≤4时,如图2,易得PD=CD=4﹣x,根据三角形面积公式得到y=﹣![]() x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
x2+2x,于是可判断当0≤x≤2时,y与x的函数关系的图象为开口向上的抛物线的一部分,当2<x≤4时,y与x的函数关系的图象为开口向下的抛物线的一部分,然后利用此特征可对四个选项进行判断.
解:过A点作AH⊥BC于H,
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,BH=CH=AH=![]() BC=2,
BC=2,
当0≤x≤2时,如图1,
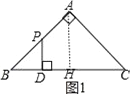
∵∠B=45°,
∴PD=BD=x,
∴y=![]() xx=
xx=![]() x2;
x2;
当2<x≤4时,如图2,
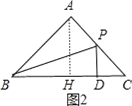
∵∠C=45°,
∴PD=CD=4﹣x,
∴y=![]() (4﹣x)x=﹣
(4﹣x)x=﹣![]() x2+2x,
x2+2x,
故选B
“点睛”本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力,解决本题的关键是利用分类讨论的思想求出y与x的函数关系.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】根据所学知识完成小题:
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.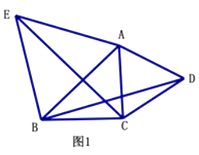
(2)【深入探究】如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.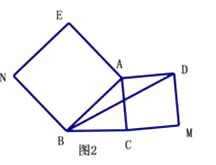
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:在平面直角坐标系![]() 中,一张矩形纸片
中,一张矩形纸片![]() 按图
按图![]() 所示放置.已知
所示放置.已知![]() ,
, ![]() ,将这张纸片折叠,使点
,将这张纸片折叠,使点![]() 落在边
落在边![]() 上,记作点
上,记作点![]() ,折痕与边
,折痕与边![]() (含端点).
(含端点).
交于点![]() ,与边
,与边![]() (含端点)或其延长线交于点
(含端点)或其延长线交于点![]() .
.
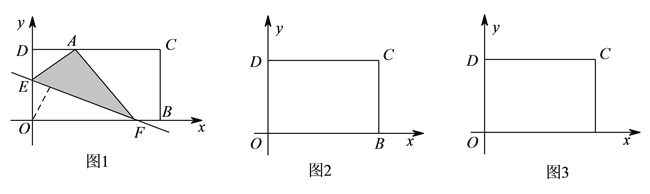
问题探究:
(![]() )如图
)如图![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,直接写出点
,直接写出点![]() 的坐标________;
的坐标________;
(![]() )将矩形沿直线
)将矩形沿直线![]() 折叠,求点
折叠,求点![]() 的坐标;
的坐标;
问题解决:
(![]() )将矩形沿直线
)将矩形沿直线![]() 折叠,点
折叠,点![]() 在边
在边![]() 上(含端点),求
上(含端点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量( ) 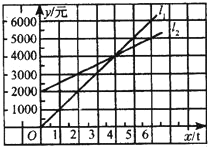
A.小于3t
B.大于3t
C.小于4t
D.大于4t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,西部地区最大的客运枢纽系统﹣﹣重庆西站,一期工程已经完成90%,预计在年内建成投入使用.届时,预计每年客流量可达42000000人次,将数42000000用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售A,B两种商品,已知销售一件A种商品可获利润10元,销售一件B种商品可获利润15元.
(1)该商店销售A,B两种商品共100件,获利润1350元,则A,B两种商品各销售多少件?
(2)根据市场需求,该商店准备购进A,B两种商品共200件,其中B种商品的件数不多于A种商品件数的3倍.为了获得最大利润,应购进A,B两种商品各多少件?可获得最大利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com