
【题目】某商店销售A,B两种商品,已知销售一件A种商品可获利润10元,销售一件B种商品可获利润15元.
(1)该商店销售A,B两种商品共100件,获利润1350元,则A,B两种商品各销售多少件?
(2)根据市场需求,该商店准备购进A,B两种商品共200件,其中B种商品的件数不多于A种商品件数的3倍.为了获得最大利润,应购进A,B两种商品各多少件?可获得最大利润为多少元?
【答案】
(1)解:设A种商品销售x 件,
则B种商品销售(100-x)件.
依题意,得 10x+15(100-x)=1350
解得x=30.
∴100-x=70.
答:A种商品销售30件,B种商品销售70件
(2)解:设购进A种商品m件,则购进B商品(200-m)件,根据题意的
0≤200-m≤3m
解之:200≤m≤50
设所获利润为W元,根据题意得
w=10m+15(200-m)=-5m+3000
∵-5<0.
∴w随m的增大而减小,
∴当m=50时,所得利润最大
∴w=-5×50+3000=2750
200-m=150
答:为了获得最大利润,应购进A商品50件,应购进B商品150件,可获得最大利润为2750元。
【解析】(1)此题等量关系是:A商品的件数+B商品=100;每件A商品的利润![]() A商品的数量+每件B商品的利润
A商品的数量+每件B商品的利润![]() B商品的数量=1350;建立方程或出租。求解即可。
B商品的数量=1350;建立方程或出租。求解即可。
(2)根据题意可得不等关系:0≤B种商品的件数≤3![]() A种商品件数,建立不等式组求解即可;设所获利润为W元,得出w=每件A商品的利润
A种商品件数,建立不等式组求解即可;设所获利润为W元,得出w=每件A商品的利润![]() A商品的数量+每件B商品的利润
A商品的数量+每件B商品的利润![]() B商品的数量,建立函数解析式,再根据一次函数的性质求出结果即可。
B商品的数量,建立函数解析式,再根据一次函数的性质求出结果即可。


科目:初中数学 来源: 题型:
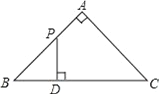
【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A. 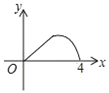 B.
B. 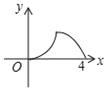 C.
C. 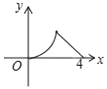 D.
D. 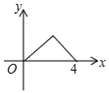
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八届五中全会出台了全面实施一对夫妇可生育两个孩子的政策,这是党中央站在中华民族长远发展的战略高度作出的促进人口长期均衡发展的重大举措.二孩政策出台后,某家庭积极响应政府号召,准备生育两个小孩(生男生女机会均等,且与顺序有关).
(1)该家庭生育两胎,假设每胎都生育一个小孩,求这两个小孩恰好是1男1女的概率;
(2)该家庭生育两胎,假设第一胎生育一个小孩,且第二胎生育一对双胞胎,求这三个小孩中至少有1个女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
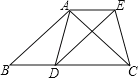
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:AD=CE;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:对称轴x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(﹣3,0),且点(2,5)在抛物线y=ax2+bx+c上.
(1)求抛物线的解析式.
(2)点C为抛物线与y轴的交点.
①点P在抛物线上,且S△POC=4S△BOC,求点P点坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com