
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.

【答案】(1)见解析;(2)11.
【解析】分析:(1)连接OD,由D为弧BC的中点,得到两条弧相等,进而得到两个同位角相等,确定出OD与AE平行,利用两直线平行同旁内角互补得到OD与DE垂直,即可得证;
(2)过O作OF垂直于AC,利用垂径定理得到F为AC中点,再由四边形OFED为矩形,求出FE的长,由AF+EF求出AE的长即可.
详解:(1)连接OD,

∵D为弧BC的中点,∴弧BD=弧CD,
∴∠BOD=∠BAE,∴OD∥AE,
∵DE⊥AC,∴∠ADE=90°,∴∠AED=90°,
∴OD⊥DE,
则DE为圆O的切线;
(2)过点O作OF⊥AC,
∵AC=10,∴AF=CF=![]() AC=5,
AC=5,
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED为矩形,
∴FE=OD=![]() AB,
AB,
∵AB=12,∴FE=6,
则AE=AF+FE=5+6=11.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△A0B的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )

A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ABC=90°.

(1)先作∠ACB的平分线;设它交AB边于点O,再以点O为圆心,OB为半径作⊙O(尺规作图,保留作图痕迹,不写作法);
(2)证明:AC是所作⊙O的切线;
(3)若BC=![]() ,∠A=30°,求△AOC的面积.
,∠A=30°,求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.

(1)求点O到BD的距离及∠OBD的度数;
(2)若DE=2BE,求![]() 的值和CD的长.
的值和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
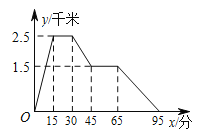
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com