
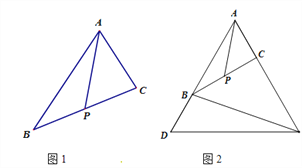
【题目】试解答下列问题:
(1)在图1我们称之为“8字形”,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3) 在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .

【答案】(1)∠A+∠D=∠C+∠B;(2)6;(3)38°;(4)2∠P=∠D+∠B;
【解析】试题分析:(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;
(2)根据“8字形”的定义,仔细观察图形即可得出“8字形”共有6个;
(3)先根据“8字形”中的角的规律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根据角平分线的定义,得出∠DAP=∠PAB,∠DCP=∠PCB,将①+②,可得2∠P=∠D+∠B,进而求出∠P的度数;
(4)同(3),根据“8字形”中的角的规律及角平分线的定义,即可得出2∠P=∠D+∠B.
解:(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
故答案为:∠A+∠D=∠C+∠B;
(2)①线段AB、CD相交于点O,形成“8字形”;
②线段AN、CM相交于点O,形成“8字形”;
③线段AB、CP相交于点N,形成“8字形”;
④线段AB、CM相交于点O,形成“8字形”;
⑤线段AP、CD相交于点M,形成“8字形”;
⑥线段AN、CD相交于点O,形成“8字形”;
故“8字形”共有6个;
故答案为:6;
(3)∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B,
又∵∠D=40度,∠B=36度,
∴2∠P=40°+36°,
∴∠P=38°;
(4)关系:2∠P=∠D+∠B
由∠D+∠1+∠2=∠B+∠3+∠4①
由∠ONC=∠B+∠4=∠P+∠2,②
①+②得:
∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1,
∠D+2∠B=2∠P+∠B,
即2∠P=∠D+∠B.
故答案为:2∠P=∠D+∠B.



科目:初中数学 来源: 题型:
【题目】将抛物线y=3x2向左平移2个单位,再向下平移1个单位,所得抛物线为( )
A. y=3(x-2)2-1 B. y=3(x-2)2+1 C. y=3(x+2)2-1 D. y=3(x+2)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位急需用车,但不准备买车,他们准备和一个体车主或一国营出租车公司中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是![]() 元,应付给国营出租车公司的月租费是
元,应付给国营出租车公司的月租费是![]() 元,
元, ![]() ,
, ![]() 分别与
分别与![]() 之间的函数关系的图象(两条射线)如图所示,观察图象,回答下列问题.
之间的函数关系的图象(两条射线)如图所示,观察图象,回答下列问题.
(1)分别写出![]() ,
, ![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)每月行驶的路程在什么范围内时,租国营公司的车合算?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础。结合数轴与绝对值的知识回答下列问题:
![]()
(1)数轴上表示1和4的两点之间的距离是______;表示-3和2的两点之间的距离是______;
表示数a和-2的两点之间的距离是3,那么a=________;一般地,数轴上表示数a和数b的两点之间的距离等于__________.
(2)若数轴上表示数a的点位于-4与2之间,则![]() =_______.
=_______.
(3)是否存在数a,使代数式![]() 的值最小?如果存在,请写出数a=______,此时代数式
的值最小?如果存在,请写出数a=______,此时代数式![]() 的最小值是__________.
的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠C=70°,∠B=40°,求∠DAE的度数
(2)若∠C-∠B=30°,则∠DAE=________.
(3)若∠C-∠B=![]() (∠C>∠B),求∠DAE的度数(用含
(∠C>∠B),求∠DAE的度数(用含![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:如图1,在△![]() 中,点
中,点![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() <
<![]() 小明提供了他研究这个问题的思路:从点
小明提供了他研究这个问题的思路:从点![]() 为
为![]() 的中点出发,可以构造以
的中点出发,可以构造以![]() 、
、![]() 为邻边的平行四边形
为邻边的平行四边形![]() ,结合平行四边形的性质以及三角形两边之和大于第三边的性质便可解决这个问题.请结合小明研究问题的思路,解决下列问题:
,结合平行四边形的性质以及三角形两边之和大于第三边的性质便可解决这个问题.请结合小明研究问题的思路,解决下列问题:
(1)完成上面问题的解答;
(2)如果在图1中,∠![]() =60°,延长
=60°,延长![]() 到
到![]() ,使得
,使得![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() ,连结
,连结![]() ,如图2. 请猜想线段
,如图2. 请猜想线段![]() 与线段
与线段![]() 之间的数量关系.并加以证明.
之间的数量关系.并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com