
【题目】如图,在平行四边形![]() 中,
中,![]() 于
于![]() 为
为![]() 的中点,则
的中点,则![]() 的大小是( )
的大小是( )
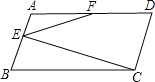
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
过F作AB的平行线FG,由于F是AD的中点,那么G是BC的中点,即Rt△BCE斜边上的中点,由此可得BC=2EG=2FG,即△GEF、△BEG都是等腰三角形,因此求∠B的度数,只需求得∠BEG的度数即可;易知四边形ABGF是平行四边形,得∠EFG=∠AEF,由此可求得∠FEG的度数,即可得到∠AEG的度数,根据邻补角的定义可得∠BEG的度数,由此得解.
解:过F作FG∥AB交BC于G,连接EG,
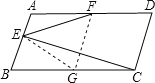
∵在平行四边形ABCD中,AB∥CD,AD∥BC,
∴FG∥AB∥CD,
∵FG∥AB,AD∥BC,
∴四边形ABGF是平行四边形,
∴AF=BG,
又∵F为AD中点
∴G是BC的中点;
∵BC=2AB,F为AD的中点,
∴BG=AB=FG=AF,
∵在Rt△BEC中,EG是斜边上的中线,
∴BG=GE=FG=![]() BC;
BC;
∴∠BEG=∠B=72°,
∴∠AEG=∠AEF+∠FEG=180°﹣∠BEG=108°,
∵AE∥FG,
∴∠EFG=∠AEF,
∵GE=FG,
∴∠EFG=∠FEG,
∴∠AEF=∠FEG=![]() ∠AEG=54°,
∠AEG=54°,
故选:A.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
关于三角函数还有如下的公式:
sin(α±β)=sin αcos β±cos αsin β
tan(α±β)= ![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan 15°=tan(45°-30°)=  =2-
=2-![]() .
.
根据以上阅读材料,请选择适当的公式解答下面问题:
(1)计算sin 15°的值.
(2)乌蒙铁塔是六盘水市标志性建筑物之一,小华想用所学的知识来测量该铁塔的高度.如图,小华站在离铁塔底A距离7 m的C处,测得铁塔顶B的仰角为75°,小华的眼睛离地面的距离DC为1.62 m,请帮助小华求出乌蒙铁塔的高度.(结果精确到0.1 m.参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图.
(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?
(2)汽车在点A的速度是多少?在点C呢?
(3)司机在第28分钟开始匀速先行驶了4分钟,之后立即以减速行驶2分钟停止,请你在本图中补上从28分钟以后汽车速度与行驶时间的关系图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
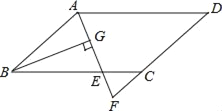
A. 8 B. 9.5 C. 10 D. 11.5
查看答案和解析>>
科目:初中数学 来源: 题型:
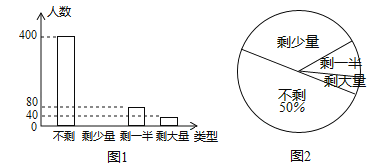
【题目】某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图 1 和图 2 所示的不完整统计图 .
(1) 被调查员工的人数为 人:
(2) 把条形统计图补充完整;
(3) 若该企业有员工 10000 人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
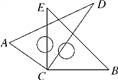
【题目】如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
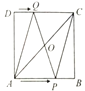
【题目】(1)已知四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正方形边上的两个动点,点
是正方形边上的两个动点,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向运动,点
方向运动,点![]() 同时从点
同时从点![]() 出发以
出发以![]() 速度沿
速度沿![]() 方向运动.设点
方向运动.设点![]() 运动的时间为
运动的时间为![]() .
.
①如图1,点![]() 在
在![]() 边上,
边上,![]() 相交于点
相交于点![]() ,当
,当![]() 互相平分时,求
互相平分时,求![]() 的值;
的值;
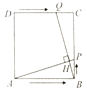
②如图2,点![]() 在
在![]() 边上,
边上,![]() 相交于点
相交于点![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
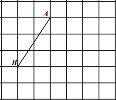
(2)如图,在小正方形的边长为1的正方形网格中,点![]() 在格点上.
在格点上.
①线段![]() 的长是_____________;
的长是_____________;
②在网格中用无刻度的直尺,以![]() 为边画矩形
为边画矩形![]() ,使这个矩形的面积是
,使这个矩形的面积是![]() .
.
要求:保留画图痕迹,并说明点![]() 的位置如何找到的.
的位置如何找到的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长为1个单位长度,建立如图所示的平面直角坐标系,△ABC的顶点均为格点,把△ABC向右平移5个单位长度得到△A1B1C1,再作出△ABC关于x轴对称的△A2B2C2.
(1)在图中画出△A1B1C1和△A2B2C2;
(2)点![]() 在
在![]() 轴上,且△ABP与△ABC的面积相等,则点P坐标为______;
轴上,且△ABP与△ABC的面积相等,则点P坐标为______;
(3)横、纵坐标均为整数的点为整数点,在第二象限中的整数点M满足OM<OC,直接写出整数点![]() 的所有可能坐标.
的所有可能坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在画有方格图的平面直角坐标系中,△ABC的三个顶点均在格点上.
(1)将△ACB绕点B顺时针方向旋转![]() ,在方格图中用直尺画出旋转后对应的△A1C1B,则A1点的坐标是(_________),C1点的坐标是(_________).
,在方格图中用直尺画出旋转后对应的△A1C1B,则A1点的坐标是(_________),C1点的坐标是(_________).
(2)在方格图中用直尺画出△ACB关于原点O的中心对称图形△A2C2B2,则A2点的坐标是(_________),C2点的坐标是(_________).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com