
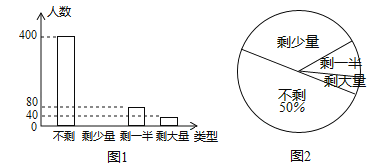
【题目】某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图 1 和图 2 所示的不完整统计图 .
(1) 被调查员工的人数为 人:
(2) 把条形统计图补充完整;
(3) 若该企业有员工 10000 人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
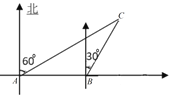
【题目】如图,某货船以24海里/时的速度将一批重要物资从![]() 处运往正东方向的M处,在点
处运往正东方向的M处,在点![]() 处测得某岛
处测得某岛![]() 在北偏东
在北偏东![]() 的方向上.该货船航行
的方向上.该货船航行![]() 分钟后到达
分钟后到达![]() 处,此时再测得该岛在北偏东
处,此时再测得该岛在北偏东![]() 的方向上,已知在
的方向上,已知在![]() 岛周围
岛周围![]() 海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=BC;(3)BD平分∠ABC;(4)AO=CO.其中正确的有______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
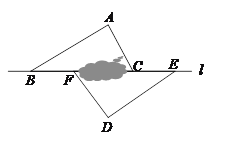
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边的中点,点E,F分别在AC,AB上,且DE∥AB,EF∥BC.
(1)求证:CD=EF;
(2)已知∠ABC=60°,连接BE,若BE平分∠ABC,CD=6,求四边形BDEF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图像交y轴于C点,交
的图像交y轴于C点,交![]() 轴于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程![]() 的两个根.
的两个根.
(1)求出点A、点B的坐标及该二次函数表达式.

(2)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合),过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
(3)如图3,线段MN是直线y=x上的动线段(点M在点N左侧),且MN=![]() ,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由.
,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OE平分∠BOD,∠AOC=70°,∠DOF=90°.

(1)图中与∠EOF互余的角是 ;
(2)求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com