
 证明:设△ABC外接圆半径为1,三个内角记为A,B,C.
证明:设△ABC外接圆半径为1,三个内角记为A,B,C.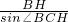 =2,
=2, ,由此可以得到AH1=sinB•AB=sinB•(2sinC)=2sinB•sinC,接着可以得到3d重=△ABC三条高的和=2•(sinB•sinC+sinC•sinA+sinA•sinB),而,所以
,由此可以得到AH1=sinB•AB=sinB•(2sinC)=2sinB•sinC,接着可以得到3d重=△ABC三条高的和=2•(sinB•sinC+sinC•sinA+sinA•sinB),而,所以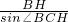 =2;由此可知HH1=cosC•BH=2•cosB•cosC,d垂=HH1+HH2+HH3=2(cosB•cosC+cosC•cosA+cosA•cosB),最后代入1•d垂+2•d外=3•d重.即可证明结论.
=2;由此可知HH1=cosC•BH=2•cosB•cosC,d垂=HH1+HH2+HH3=2(cosB•cosC+cosC•cosA+cosA•cosB),最后代入1•d垂+2•d外=3•d重.即可证明结论.

科目:初中数学 来源: 题型:
| aha | a+ha |
查看答案和解析>>
科目:初中数学 来源: 题型:
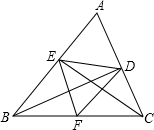 在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DF=EF;②AD:AB=AE:AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45°时,BE=
在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DF=EF;②AD:AB=AE:AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45°时,BE=| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com