
【题目】如图,直线AB:y=-x-b分别与x、y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于点C,且OB:OC=3:1.
(1)求直线BC的解析式;
(2)如图,P为A点右侧x轴上的一动点,以P为直角顶点,BP为腰在第一象限内作等腰直角△BPQ,连接QA并延长交y轴于点K,当P点运动时,K点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请说明理由.

【答案】(1)y=3x+6(2)K点的位置不发生变化,K(0,6),理由见解析
【解析】
(1)设BC的解析式是y=ax+c,由直线AB:y=xb过A(6,0),可以求出b,因此可以求出B点的坐标,再由已知条件可求出C点的坐标,把B,C点的坐标分别代入求出a和c的值即可;
(2)过Q作QH⊥x轴于H,首先证明△BOP≌△PHQ,再分别证明△AHQ和△AOK为等腰直角三角形,问题得解.
(1)由已知:0=6b,
∴b=6,
∴AB:y=x+6.
∴B(0,6),
∴OB=6,
∵OB:OC=3:1,
OC=![]() =2,
=2,
∴C(2,0),
设BC的解析式是y=ax+c,代入得![]() ,
,
解得:![]() ,
,
∴直线BC的解析式是:y=3x+6;
(2)K点的位置不发生变化,K(0,6).
过Q作QH⊥x轴于H,
∵△BPQ是等腰直角三角形,
∴∠BPQ=90°,PB=PQ,
∵∠BOA=∠QHA=90°,
∴∠BPO=∠PQH,
∴△BOP≌△PHQ,
∴PH=BO,OP=QH,
∴PH+PO=BO+QH,
即OA+AH=BO+QH,
又OA=OB,
∴AH=QH,
∴△AHQ是等腰直角三角形,
∴∠QAH=45°,
∴∠OAK=45°,
∴△AOK为等腰直角三角形,
∴OK=OA=6,
∴K(0,6).



科目:初中数学 来源: 题型:
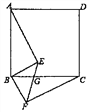
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE. 
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于点A(﹣5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.
(1)求抛物线的解析式;
(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF= ![]() ,求点Q的坐标;
,求点Q的坐标;
(3)在矩形的平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与双曲线y= ![]() (k≠0,且x>0)交于点A,点A的横坐标是1.
(k≠0,且x>0)交于点A,点A的横坐标是1.
(1)求点A的坐标及双曲线的解析式;
(2)点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com