
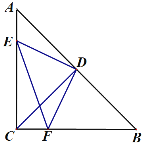
【题目】如图在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,点E、F分别在AC、BC上,且∠EDF=90°.
(1)求证:△AED≌△CFD;
(2)试判断CE、CF与CD之间的数量关系,并说明理由;
(3)若CF=1,CE=3,试求DF的长.
【答案】(1)证明见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)由等腰直角三角形的性质得到AD=BD=CD,∠A=∠B=∠DCF=45°.再由同角的余角相等得到∠ADE=∠CDF.用ASA即可证明△AED≌△CFD;
(2)由全等三角形的性质和等腰直角三角形的性质即可得出CE+CF=![]() AD;
AD;
(3)过D作DG⊥CA于G.由△AED≌△CDF可以求得AC、AD的长,再由等腰直角三角形的性质得出AG、DG的长,从而得到EG的长,再DF=ED和勾股定理即可得出结论.
(1)∵∠ACB=90°,AC=BC,∴△ABC是等腰直角三角形.
∵CD⊥AB,∴AD=BD=CD,∠A=∠B=∠DCF=45°.
∵∠EDF=90°,∴∠EDC+∠CDF=∠EDC+∠ADE=90°,∴∠ADE=∠CDF.
在△AED和△CDF中,∵ ∠ADE=∠CDF,AD=CD,∠A=∠DCF,∴△AED≌△CFD;
(2)∵△AED≌△CFD,∴AE=CF,∴CE+CF=CE+AE=AC.
∵△ADC是等腰直角三角形,∴AC=![]() AD,∴CE+CF=
AD,∴CE+CF=![]() AD;
AD;
(3)过D作DG⊥CA于G.由(2)得:△AED≌△CFD ,AC=CE+CF=4,CE+CF=![]() AD,∴ED=FD,3+1=
AD,∴ED=FD,3+1=![]() AD,解得:AD=
AD,解得:AD=![]() .
.
∵∠A=45°,∴△AGD是等腰直角三角形,∴AG=DG=2.
∵AE=CF=1,∴EG=AG-AE=2-1=1,∴DF=ED=![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
图1

图2

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.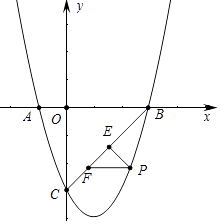
(1)求抛物线的解析式;
(2)如图所示,直线BC下方的抛物线上有一点P,过点p作PE⊥BC于点E,作PF平行于x轴交直线BC于点F,求△PEF周长的最大值;
(3)已知点M是抛物线的顶点,点N是y轴上一点,点Q是坐标平面内一点,若点P是抛物线上一点,且位于抛物线的对称轴右侧,是否存在以P、M、N、Q为顶点且以PM为边的正方形?若存在,直接写出点P的横坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y1= ![]() (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=
(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2= ![]() (x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2﹣k1的值为( )
(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2﹣k1的值为( )
A.﹣2
B.2
C.﹣4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校2400名学生的阅读兴趣,从中随机抽查了部分同学,就“我最感兴趣的书籍”进行了调查:A.小说、B.散文、C.科普、D.其他(每个同学只能选择一项),进行了相关统计,整理并绘制出两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
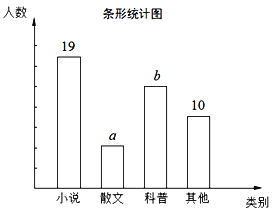

(1)本次抽查中,样本容量为______;
(2)a=______,b=______;
(3)扇形统计图中,其他类书籍所在扇形的圆心角是______°;
(4)请根据样本数据,估计全校有多少名学生对散文感兴趣.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某农场有A、B两种型号的收割机共20台,每台A型收割机每天可收大麦100亩或者小麦80亩,每台B型收割机每天可收大麦80亩或者小麦60亩,该农场现有19 000亩大麦和11 500亩小麦先后等待收割.先安排这20台收割机全部收割大麦,并且恰好10天时间全部收完.
(1)问A、B两种型号的收割机各多少台?
(2)由于气候影响,要求通过加班方式使每台收割机每天多完成10%的收割量,问这20台收割机能否在一周时间内完成全部小麦收割任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com