
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(8分)

(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 .
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 .
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-4,-3
①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
【答案】(1)无理;-π;(2)±4π;(3)①第4次;第3次;②26π;-6π .
【解析】
试题分析:(1)利用圆的半径以及滚动周数即可得出滚动距离;(2)利用圆的半径以及滚动周数即可得出滚动距离,注意两个方向;(3)①利用滚动的方向以及滚动的周数即可得出A点移动距离变化;②利用绝对值的性质以及有理数的加减运算得出移动距离和A表示的数即可.
试题解析:(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C到原点的距离是半圆周长,圆半径为1,所以点C表示的数是无理数,这个数是-π;故答案为:无理,-π;(2)把圆片沿数轴滚动2周,向左或向右,点A到达数轴上点D的位置,点D到原点的距离是两个圆周长,半径还是1,故点D表示的数是4π或-4π;故答案为:4π或-4π;(3)①∵圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-4,-3,因为(+2)+(-1)+(+3)+(-4)=0,∴第4次滚动后,A点距离原点最近,因为(+2)+(-1)+(+3)=4,所以第3次滚动后,A点距离原点最远;②∵A点运动的圆周数为:|+2|+|-1|+|+3|+|-4|+|-3|=13,∴13×2π×1=26π,∴A点运动的路程共有26π;∵(+2)+(-1)+(+3)+(-4)+(-3)=-3,(-3)×2π=-6π,∴此时点A所表示的数是:-6π.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
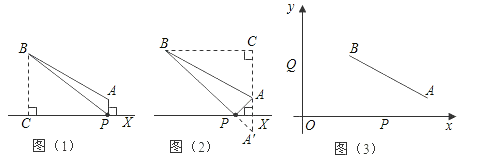
【题目】(满分8分)恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷![]() 和世界级自然保护区星斗山
和世界级自然保护区星斗山![]() 位于笔直的沪渝高速公路X同侧,
位于笔直的沪渝高速公路X同侧, ![]() 、
、![]() 到直线x的距离分别为
到直线x的距离分别为![]() 和
和![]() ,要在沪渝高速公路旁修建一服务区
,要在沪渝高速公路旁修建一服务区![]() ,向
,向![]() 、
、![]() 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(
两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(![]() 与直线x垂直,垂足为
与直线x垂直,垂足为![]() ),
),![]() 到
到![]() 、
、![]() 的距离之和
的距离之和![]() ,图(2)是方案二的示意图(点
,图(2)是方案二的示意图(点![]() 关于直线x的对称点是
关于直线x的对称点是![]() ,连接
,连接![]() 交直线x于点
交直线x于点![]() ),
),![]() 到
到![]() 、
、![]() 的距离之和
的距离之和![]() .
.
(1)求![]() 、
、![]() ,并比较它们的大小;
,并比较它们的大小;
(2)请你说明![]() 的值为最小;
的值为最小;
(3)拟建的恩施到张家界高速公路Y与沪渝高速公路垂直,建立如图(3)所示的直角坐标系, ![]() 到直线Y的距离为
到直线Y的距离为![]() ,请你在X旁和Y旁各修建一服务区
,请你在X旁和Y旁各修建一服务区![]() 、
、![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 组成的四边形的周长最小.并求出这个最小值.
组成的四边形的周长最小.并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察一列数a1=3,a2=32,a3=33,a4=34,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是_______;根据此规律,如果an(n为正整数)表示这个数列的第n项,那么a6=_______,an=_______;(可用幂的形式表示)
(2)如果想要求l+2+22+23+...+210的值,可令S10=l+2+22+23+...+210①,将①式两边同乘以2,得_______②,由②减去①式,得S10=_______.
(3)若(1)中数列共有20项,设S20=3+32+33+34+…+320,请利用上述规律和方法计算S20的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润![]() (万元)与投资成本x(万元)满足如图①所示的二次函数
(万元)与投资成本x(万元)满足如图①所示的二次函数![]() ;种植柏树的利润
;种植柏树的利润![]() (万元)与投资成本x(万元)满足如图②所示的正比例函数
(万元)与投资成本x(万元)满足如图②所示的正比例函数![]() =kx.
=kx.
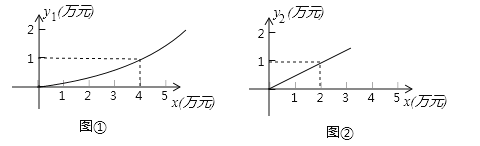
(1)分别求出利润![]() (万元)和利润
(万元)和利润![]() (万元)关于投资成本x(万元)的函数关系式;
(万元)关于投资成本x(万元)的函数关系式;
(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
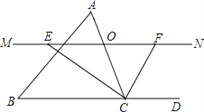
【题目】如图,在△ABC中,点O是边AC上一个动点(不与点A、C重合),过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)探究OE与OF的数量关系并加以证明;
(2)当点O在边AC上运动到什么位置,四边形AECF是矩形,请说明理由;
(3)在第(2)问的基础上,△ABC满足什么条件时,四边形AECF是正方形?(不需说明理由)
(4)当点O在边AC上运动时,四边形BCFE能成为菱形吗?若能,请加以证明;若不能,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
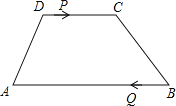
【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com