
分析 (1)先进行二次根式的化简,然后合并;
(2)先进行二次根式的乘法运算与化简,然后合并;
(3)先进行平方差公式和二次根式的化简,然后合并;
(4)直接根据完全平方公式进行运算;
(5)先进行二次根式的化简,然后合并;
(6)先开方,然后求出方程的解.
解答 解:(1)原式=3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$+2$\sqrt{3}$
=$\frac{14}{3}$$\sqrt{3}$;
(2)原式=3$\sqrt{2}$-6$\sqrt{5}$-3$\sqrt{2}$
=-6$\sqrt{5}$;
(3)原式=3-2-5
=-4;
(4)原式=12-4+$\frac{1}{3}$
=$\frac{25}{3}$;
(5)原式=6-3+2
=5;
(6)开平方得:3x-1=±5,
解得:x=2或x=-$\frac{4}{3}$.
点评 本题考查了实数的运算,涉及了二次根式的乘法运算、平方差公式、完全平方公式、二次根式的化简与合并等知识点,掌握运算法则是解答本题的关键.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:解答题
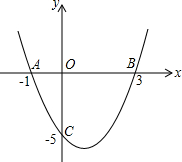 如图:已知二次函数的图象经过点A(-1,0),B(3,0),C(0,-5),
如图:已知二次函数的图象经过点A(-1,0),B(3,0),C(0,-5),查看答案和解析>>
科目:初中数学 来源: 题型:填空题
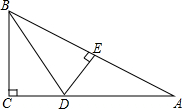 如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3:8,则△ADE与△BCA的面积之比1:4.
如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于E,若△BCD与△BCA的面积比为3:8,则△ADE与△BCA的面积之比1:4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
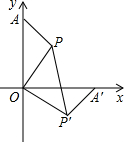 如图所示,在直角坐标系中,点A(0,9),点P(4,6),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则PP′=2$\sqrt{26}$.
如图所示,在直角坐标系中,点A(0,9),点P(4,6),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则PP′=2$\sqrt{26}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com