
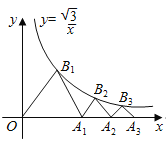
【题目】如图,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,都是一边在
,都是一边在![]() 轴上的等边三角形,点
轴上的等边三角形,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都在反比例函数
都在反比例函数![]() 的图象上,点
的图象上,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,都在
,都在![]() 轴上,则
轴上,则![]() 的坐标为________.
的坐标为________.
【答案】![]()
【解析】
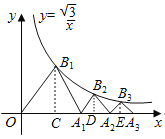
如图,过点B1作B1C⊥x轴于点C,过点B2作B2D⊥x轴于点D,过点B3作B3E⊥x轴于点E,先在△OCB1中,表示出OC和B1C的长度,表示出B1的坐标,代入反比例函数,求出OC的长度和OA1的长度,表示出A1的坐标,同理可求得A2、A3的坐标,即可发现一般规律.
如图,过点B1作B1C⊥x轴于点C,过点B2作B2D⊥x轴于点D,过点B3作B3E⊥x轴于点E,
∵△OA1B1为等边三角形,
∴∠B1OC=60°,
∴![]() ,B1C=
,B1C= ![]() OC,
OC,
设OC的长度为x,则B1的坐标为(![]() ),代入函数关系式可得:
),代入函数关系式可得:![]() ,
,
解得,x=1或x=-1(舍去),
∴OA1=2OC=2,
∴A1(2,0)
设A1D的长度为y,同理,B2D为![]() y,B2的坐标表示为
y,B2的坐标表示为![]() ,
,
代入函数关系式可得![]() ,
,
解得:y=![]() 或y=
或y=![]() (舍去)
(舍去)
∴A1D=![]() ,A1A2=
,A1A2=![]() ,OA2=
,OA2=![]()
∴A2(![]() ,0)
,0)
设A2E的长度为z,同理,B3E为![]() z,B3的坐标表示为
z,B3的坐标表示为![]() ,
,
代入函数关系式可得![]() ,
,
解得:z=![]() 或z=
或z=![]() (舍去)
(舍去)
∴A2E=![]() ,A2A3=
,A2A3=![]() ,OA3=
,OA3=![]()
∴A3(![]() ,0),
,0),
综上可得:An(![]() ,0),
,0),
故答案为:![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】某体育器材专卖柜经销A、B两种器材,A种器材每件进价350元,售价480元;B种器材每件进价200元,售价300元.
(1)该专卖柜计划用8000元去购进A、B两种器材若干件.
①若购进A种器材x件,B种器材y件,所获利润w元,请写出w与x之间满足的函数关系式;
②怎样购进才能使专卖柜经销这两种器材所获利润最大(其中A种器材不少于7件)?
(2)在“五·一”期间,该专卖柜对A、B两种器材进行如下优惠促销活动:
一次性购物总金额 | 优惠措施 |
不超过3000元 | 不优惠 |
超过3000元不超过4000元 | 售价打八折 |
超过4000元 | 售价打七折 |
促销活动期间:甲学校去该专卖柜购买A种器材付款2688元;乙学校去该专卖柜购买B种器材付款2100元,求丙学校决定一次性购买甲学校和乙学校购买的同样多的器材需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 为对角线
为对角线![]() 的中点.
的中点.
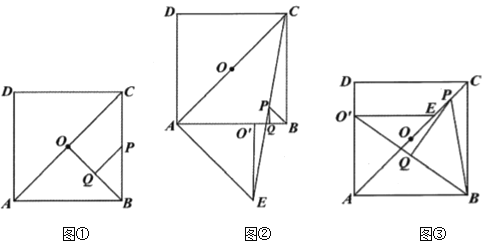
(1)问题解决:如图①,连接![]() ,分别取
,分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连接
,连接![]() ,则
,则![]() 与
与![]() 的数量关系是_____,位置关系是____;
的数量关系是_____,位置关系是____;
(2)问题探究:如图②,![]() 是将图①中的
是将图①中的![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到的三角形,连接
得到的三角形,连接![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .判断
.判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(3)拓展延伸:如图③,![]() 是将图①中的
是将图①中的![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到的三角形,连接
得到的三角形,连接![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() .若正方形
.若正方形![]() 的边长为1,求
的边长为1,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC,∠ABC=90°,顶点A在第一象限,B、C在x轴的正半轴上(C在B的右侧),BC=3,AB=4,若双曲线![]() 交边AB于点E,交边AC于中点D.
交边AB于点E,交边AC于中点D.
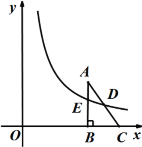
(1)若OB=2,求k;
(2)若AE=![]() , 求直线AC的解析式.
, 求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线![]() 与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
与x轴相交于A、B两点,与y轴相交于点C,点M为抛物线的顶点.
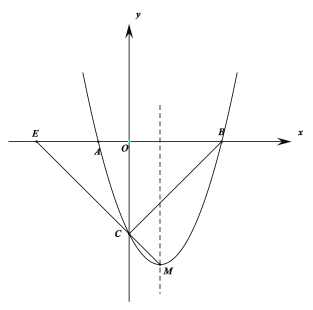
(1)求点C及顶点M的坐标.
(2)若点N是第四象限内抛物线上的一个动点,连接![]() 求
求![]() 面积的最大值及此时点N的坐标.
面积的最大值及此时点N的坐标.
(3)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(4)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P、E、O为顶点的三角形与![]() 相似.若存在,求出点P的坐标;若不存在,请说明理由.
相似.若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:

(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“京津冀生态建设协同发展”,我区某街道要增大绿化面积,决定从备选的五种树中选一种进行栽种.为了更好的了解民意,工作人员在街道辖区范围内随机走访了部分居民,进行“我最喜欢的一种树”的调查活动(每人选其中一种树),将调查结果整理后,绘制出下面两个不完整的统计图.


请根据所给信息回答问题:
(1)这次参与调查的居民人数为________;
(2)将条形统计图补充完整;
(3)扇形统计图中,![]() ________;“白蜡”所在扇形的圆心角度数为________;
________;“白蜡”所在扇形的圆心角度数为________;
(4)已知该街道辖区内现在居民8万人,请你估计这8万人中最喜欢“银杏”的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com