
ЁОЬтФПЁПЭМЂйЪЧИЪЫрЪЁВЉЮяЙнЕФеђЙнжЎБІЁЊЁЊЭБМТэЃЌгжГЦЁАТэЬЄЗЩбрЁБЃЌгк1969Фъ10дТГіЭСгкЮфЭўЪаЕФРзЬЈККФЙЃЌ1983Фъ10дТБЛЙњМвТУгЮОжШЗЖЈЮЊжаЙњТУгЮБъжОЃЌдкКмЖрТУгЮГЧЪаЕФЙуГЁЩЯЖМгаЁАТэЬЄЗЩбрЁБЕёЫмЃЌФГбЇЯАаЁзщАбВтСПБОГЧЪаЙуГЁЕФЁАТэЬЄЗЩбрЁБЕёЫмЃЈЭМЂкЃЉзюИпЕуРыЕиУцЕФИпЖШзїЮЊвЛДЮПЮЬтЛюЖЏЃЌЭЌбЇУЧжЦЖЈСЫВтСПЗНАИЃЌВЂЭъГЩСЫЪЕЕиВтСПЃЌВтЕУНсЙћШчЯТБэЃК
ПЮЬт | ВтСПЁАТэЬЄЗЩбрЁБЕёЫмзюИпЕуРыЕиУцЕФИпЖШ | |||
ВтСПЪОвтЭМ |
| ШчЭМЃЌЕёЫмЕФзюИпЕу | ||
ВтСПЪ§Он |
|
|
| вЧЦї |
|
| 5Уз |
| |
ЧыФуИљОнЩЯБэжаЕФВтСПЪ§ОнЃЌАяжњИУаЁзщЧѓГіЁАТэЬЄЗЩбрЁБЕёЫмзюИпЕуРыЕиУцЕФИпЖШЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉЃЎЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ


| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкУПИіБпГЄЖМЮЊ![]() ЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌаЁе§ЗНаЮЕФЖЅЕуНазіИёЕуЃЎЯпЖЮ
ЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌаЁе§ЗНаЮЕФЖЅЕуНазіИёЕуЃЎЯпЖЮ![]() ЕФЖЫЕу
ЕФЖЫЕу![]() ОљдкИёЕуЩЯЃЎ
ОљдкИёЕуЩЯЃЎ
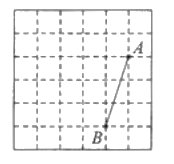
ЃЈ1ЃЉЯпЖЮ![]() ЕФГЄЖШЕШгк ЃЛ
ЕФГЄЖШЕШгк ЃЛ
ЃЈ2ЃЉНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌдкЭМжаЛГі
ЃЌдкЭМжаЛГі![]() ЃЌВЂСЌНс
ЃЌВЂСЌНс![]() ЃЎ
ЃЎ
ЃЈ3ЃЉдкЯпЖЮ![]() ЩЯШЗЖЈвЛЕу
ЩЯШЗЖЈвЛЕу![]() СЌНс
СЌНс![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() гы
гы![]() ЕФУцЛ§БШЮЊ
ЕФУцЛ§БШЮЊ![]() ЃЎ
ЃЎ
ЫЕУїЃКвдЩЯзїЭМжЛгУЮоПЬЖШЕФжБГпЛЭМЃЌБЃСєЛЭМКлМЃЃЌВЛаДЛЗЈЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛЃЌЦфжавЛИіНЛЕуЕФКсзјБъЪЧ2ЃЎ
ЕФЭМЯѓЯрНЛЃЌЦфжавЛИіНЛЕуЕФКсзјБъЪЧ2ЃЎ
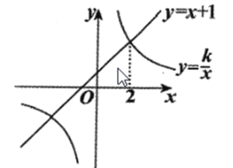
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉНЋвЛДЮКЏЪ§![]() ЕФЭМЯѓЯђЯТЦНвЦ2ИіЕЅЮЛЃЌЧѓЦНвЦКѓЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓЯђЯТЦНвЦ2ИіЕЅЮЛЃЌЧѓЦНвЦКѓЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЭМЯѓЕФНЛЕузјБъЃЛ
ЭМЯѓЕФНЛЕузјБъЃЛ
ЃЈ3ЃЉжБНгаДГівЛИівЛДЮКЏЪ§ЃЌЪЙЦфЙ§Еу![]() ЃЌЧвгыЗДБШР§КЏЪ§
ЃЌЧвгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓУЛгаЙЋЙВЕуЃЎ
ЕФЭМЯѓУЛгаЙЋЙВЕуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
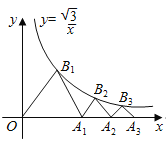
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌЖМЪЧвЛБпдк
ЃЌЖМЪЧвЛБпдк![]() жсЩЯЕФЕШБпШ§НЧаЮЃЌЕу
жсЩЯЕФЕШБпШ§НЧаЮЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЖМдкЗДБШР§КЏЪ§
ЖМдкЗДБШР§КЏЪ§![]() ЕФЭМЯѓЩЯЃЌЕу
ЕФЭМЯѓЩЯЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁЃЌ
ЃЌЁЃЌ![]() ЃЌЖМдк
ЃЌЖМдк![]() жсЩЯЃЌдђ
жсЩЯЃЌдђ![]() ЕФзјБъЮЊ________ЃЎ
ЕФзјБъЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
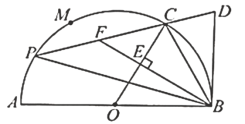
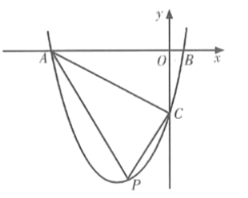
ЁОЬтФПЁПШчЭМЃЌ![]() ЮЊАыЁбOЕФжБОЖЃЌ
ЮЊАыЁбOЕФжБОЖЃЌ![]() ЃЌ
ЃЌ![]() ЪЧАыдВЩЯЕФШ§ЕШЗжЕуЃЌ
ЪЧАыдВЩЯЕФШ§ЕШЗжЕуЃЌ![]() ЃЌ
ЃЌ![]() гыАыЁбOЯрЧагкЕу
гыАыЁбOЯрЧагкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЩЯвЛЖЏЕуЃЈВЛгыЕу
ЩЯвЛЖЏЕуЃЈВЛгыЕу![]() ЃЌ
ЃЌ![]() жиКЯЃЉЃЌжБЯп
жиКЯЃЉЃЌжБЯп![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌдђЯТСаНсТле§ШЗЕФЪЧ______________ЃЎЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ
ЃЌдђЯТСаНсТле§ШЗЕФЪЧ______________ЃЎЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЮЊЖЈжЕЃЎ
ЮЊЖЈжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌНЛ
СНЕуЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌЕу
ЃЌЕу![]() ЪЧЕкШ§ЯѓЯоФкХзЮяЯпЩЯЕФвЛЖЏЕуЃЎ
ЪЧЕкШ§ЯѓЯоФкХзЮяЯпЩЯЕФвЛЖЏЕуЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉСЌНг![]() ЃЌЧѓ
ЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕМАДЫЪБЕу
УцЛ§ЕФзюДѓжЕМАДЫЪБЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчБэЪЧвЛИі4ЁС4ЃЈ4аа4СаЙВ16ИіЁАЪ§ЁБзщГЩЃЉЕФЦцУюЗНеѓЃЌДгетИіЗНеѓжабЁЫФИіЁАЪ§ЁБЃЌЖјЧветЫФИіЁАЪ§ЁБжаЕФШЮКЮСНИіВЛдкЭЌвЛааЃЌвВВЛдкЭЌвЛСаЃЌгаКмЖрбЁЗЈЃЌАбУПДЮбЁГіЕФЫФИіЁАЪ§ЁБЯрМгЃЌЦфКЭЪЧЖЈжЕЃЌдђЗНеѓжаЕкШ§ааШ§СаЕФЁАЪ§ЁБЪЧЃЈЁЁЁЁЃЉ
30 |
| 2 | 22 |
Љ3 | Љ2 | Љ | 0 |
|Љ5| | 6 | 23 | |
ЃЈ | 4 |
| ЃЈ |
A. 5 B. 6 C. 7 D. 8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгые§БШР§КЏЪ§
ЃЌгые§БШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕу
ЕФЭМЯѓНЛгкЕу![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЕФе§АыжсЩЯЃЌЧвЕу
жсЕФе§АыжсЩЯЃЌЧвЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌЗжБ№НЛвЛДЮКЏЪ§
жсЕФДЙЯпЃЌЗжБ№НЛвЛДЮКЏЪ§![]() ЕФЭМЯѓгкЕу
ЕФЭМЯѓгкЕу![]() ЃЌНЛе§БШР§КЏЪ§
ЃЌНЛе§БШР§КЏЪ§![]() ЕФЭМЯѓгкЕу
ЕФЭМЯѓгкЕу![]() ЃЎ
ЃЎ
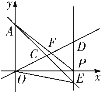
ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСЌНг![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌдкЬжТл
ЃЌдкЬжТл![]() ЕФУцЛ§гы
ЕФУцЛ§гы![]() УцЛ§ЕФДѓаЁЮЪЬтЪБЃЌМЮМЮШЯЮЊ
УцЛ§ЕФДѓаЁЮЪЬтЪБЃЌМЮМЮШЯЮЊ![]() ЃЌфПфПШЯЮЊ
ЃЌфПфПШЯЮЊ![]() ЃЌЧыФузїЮЊаЁЗЈЙйЃЌАяжњЫћУЧСНШЫЦРХаЃЌЫЕФЫЕЗЈе§ШЗЃЎ
ЃЌЧыФузїЮЊаЁЗЈЙйЃЌАяжњЫћУЧСНШЫЦРХаЃЌЫЕФЫЕЗЈе§ШЗЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
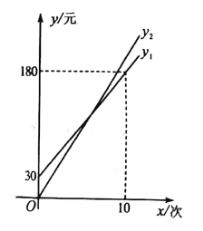
ЁОЬтФПЁПЪюЦкНЋжСЃЌФГНЁЩэОуРжВПУцЯђбЇЩњЭЦГіЪюЦкгХЛнЛюЖЏЃЌЛюЖЏЗНАИШчЯТЃЎ
ЗНАИвЛЃКЙКТђвЛеХбЇЩњЪюЦкзЈЯэПЈЃЌУПДЮНЁЩэЗбгУАДСљелгХЛнЃЛ
ЗНАИЖўЃКВЛЙКТђбЇЩњЪюЦкзЈЯэПЈЃЌУПДЮНЁЩэЗбгУАДАЫелгХЛнЃЛ
ЩшФГбЇЩњЪюЦкНЁЩэ![]() (ДЮ)ЃЌАДееЗНАИвЛЫљашЗбгУЮЊ
(ДЮ)ЃЌАДееЗНАИвЛЫљашЗбгУЮЊ![]() ЃЌ(дЊ)ЃЌЧв
ЃЌ(дЊ)ЃЌЧв![]() ЃЛАДееЗНАИЖўЫљашЗбгУЮЊ
ЃЛАДееЗНАИЖўЫљашЗбгУЮЊ![]() (дЊ) ЃЌЧв
(дЊ) ЃЌЧв![]() ЦфКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
ЦфКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
![]() Чѓ
Чѓ![]() КЭ
КЭ![]() ЕФжЕЃЌВЂЫЕУїЫќУЧЕФЪЕМЪвтвхЃЛ
ЕФжЕЃЌВЂЫЕУїЫќУЧЕФЪЕМЪвтвхЃЛ
![]() ЧѓДђелЧАЕФУПДЮНЁЩэЗбгУКЭ
ЧѓДђелЧАЕФУПДЮНЁЩэЗбгУКЭ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
![]() АЫФъМЖбЇЩњаЁЛЊМЦЛЎЪюЦкЧАЭљИУОуРжВПНЁЩэ
АЫФъМЖбЇЩњаЁЛЊМЦЛЎЪюЦкЧАЭљИУОуРжВПНЁЩэ![]() ДЮЃЌгІбЁдёФФжжЗНАИЫљашЗбгУИќЩй?ЫЕУїРэгЩЃЎ
ДЮЃЌгІбЁдёФФжжЗНАИЫљашЗбгУИќЩй?ЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com