练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如表是一个4×4（4行4列共16个“数”组成）的奇妙方阵，从这个方阵中选四个“数”，而且这四个“数”中的任何两个不在同一行，也不在同一列，有很多选法，把每次选出的四个“数”相加，其和是定值，则方阵中第三行三列的“数”是（　　）

    30

    2sin60°

    22

    ﹣3

    ﹣2

    ﹣sin45°

    0

    |﹣5|

    6

    23

    （）﹣1

    4

    （）﹣1

    A. 5 B. 6 C. 7 D. 8

    【答案】C

    【解析】分析：由表格所给的信息可知第一行为1，2，3，4；第二行为-3，-2，-1，0；第三行为5，6，7，8，由此可得结果．

    详解：∵第一行为1，2，3，4；第二行为-3，-2，-1，0；第四行为3，4，5，6

    ∴第三行为5，6，7，8，

    ∴方阵中第三行三列的“数”是7，

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某厂将四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图．

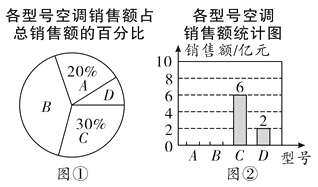
    （1）请补全图②的条形统计图；

    （2）为了应对激烈的市场竞争，该厂决定降价促销，四种型号的空调分别降价，因此该厂宣称其产品平均降价，你认为该厂的说法正确吗?请通过计算说明理由；

    （3）为进一步促销，该厂决定从这四种型号的空调中任意选取两种型号的空调降价销售，请用树状图或列表法求出降价空调中含D型号空调的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知△ABC，∠ABC=90°，顶点A在第一象限，B、C在x轴的正半轴上（C在B的右侧），BC=3，AB=4，若双曲线交边AB于点E，交边AC于中点D．

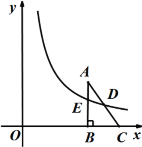
    （1）若OB=2，求k；

    （2）若AE=， 求直线AC的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马，又称“马踏飞燕”，于1969年10月出土于武威市的雷台汉墓，1983年10月被国家旅游局确定为中国旅游标志，在很多旅游城市的广场上都有“马踏飞燕”雕塑，某学习小组把测量本城市广场的“马踏飞燕”雕塑（图②）最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：

    课题

    测量“马踏飞燕”雕塑最高点离地面的高度

    测量示意图

    如图，雕塑的最高点到地面的高度为，在测点用仪器测得点的仰角为，前进一段距离到达测点，再用该仪器测得点的仰角为，且点，，，，，均在同一竖直平面内，点，，在同一条直线上．

    测量数据

    的度数

    的度数

    的长度

    仪器（）的高度

    5米

    米

    请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度（结果保留一位小数）．（参考数据：，，，，，）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点的坐标，将线段绕点按顺时针方向旋转45°，再将其长度伸长为的2倍，得到线段；又将线段绕点按顺时针方向旋转45°，长度伸长为的2倍，得到线段；如此下去，得到线段、，……，（为正整数），则点的坐标是_________．

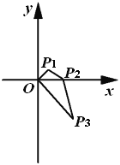
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】房山某中学改革学生的学习模式，变“老师要学生学习”为“学生自主学习”，培养了学生自主学习的能力．小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学，根据收集到的数据绘制了以下的两个统计图．请根据下面两个不完整的统计图回答以下问题：

    （1）这次抽样调查中，共调查了 名学生；

    （2）补全两幅统计图；

    （3）根据抽样调查的结果，估算该校1000名学生中大约有多少人选择“小组合作学习”？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，过点B的直线与抛物线的另一个交点为D，与抛物线的对称轴交于点E，与y轴交于点F，且，△OBE的面积为．

    （1）求抛物线的解析式；

    （2）设P为已知抛物线上的任意一点，当△ACP的面积等于△ACB的面积时，求点P的坐标；

    （3）点Q（0，m）是y轴上的动点，连接AQ、BQ，当∠AQB为钝角时，则m的取值范围是　 　．（直接写出答案）

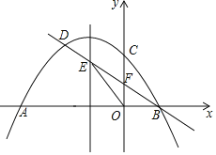
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝ax2﹣ax﹣2a（a为常数且不等于0）与x轴的交点为A，B两点，且A点在B的右侧．

    （1）当抛物线经过点（3，8），求a的值；

    （2）求A、B两点的坐标；

    （3）若抛物线的顶点为M，且点M到x轴的距离等于AB的3倍，求抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从2017年1月1日起，我国驾驶证考试正式实施新的驾考培训模式，新规定C2驾驶证的培训学时为40学时，驾校的学费标准分不同时段，普通时段a元/学时，高峰时段和节假日时段都为b元/学时．

    （1）小明和小华都在此驾校参加C2驾驶证的培训，下表是小明和小华的培训结算表（培训学时均为40），请你根据提供的信息，计算出a，b的值．

    学员

    培训时段

    培训学时

    培训总费用

    小明

    普通时段

    20

    6000元

    高峰时段

    5

    节假日时段

    15

    小华

    普通时段

    30

    5400元

    高峰时段

    2

    节假日时段

    8

    （2）小陈报名参加了C2驾驶证的培训，并且计划学够全部基本学时，但为了不耽误工作，普通时段的培训学时不会超过其他两个时段总学时的，若小陈普通时段培训了x学时，培训总费用为y元

    ①求y与x之间的函数关系式，并确定自变量x的取值范围；

    ②小陈如何选择培训时段，才能使得本次培训的总费用最低？

    查看答案和解析>>

    同步练习册答案