
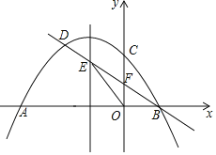
【题目】如图,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且![]() ,△OBE的面积为
,△OBE的面积为![]() .
.
(1)求抛物线的解析式;
(2)设P为已知抛物线上的任意一点,当△ACP的面积等于△ACB的面积时,求点P的坐标;
(3)点Q(0,m)是y轴上的动点,连接AQ、BQ,当∠AQB为钝角时,则m的取值范围是 .(直接写出答案)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 且
且![]()
【解析】
(1)首先根据抛物线解析式找到抛物线的对称轴,然后根据平行线分线段成比例得出HG=HO=1,OB=2,进而求出点B的坐标,然后根据△OBE的面积及平行线分线段成比例得出点D的坐标,最后利用待定系数法即可求解;
(2)首先根据抛物线的解析式求出A,C的坐标,然后利用待定系数法求出直线AC的解析式,然后设![]() ,则
,则![]() ,利用
,利用![]() ACP的面积等于
ACP的面积等于![]() ACB的面积建立一个关于m的方程,解方程求解即可;
ACB的面积建立一个关于m的方程,解方程求解即可;
(3)先利用勾股定理求出当![]() 时m的值,以及排除当A,Q,B三点共线时的m的值,即可得出当∠AQB为钝角时m的取值范围.
时m的值,以及排除当A,Q,B三点共线时的m的值,即可得出当∠AQB为钝角时m的取值范围.
解:(1)作DG⊥x轴于G,对称轴交x轴于H,如图,

∵抛物线为![]() ,
,
∴对称轴为直线x=﹣![]() =﹣1,则OH=1.
=﹣1,则OH=1.
![]()
∴OF∥EH∥DG,
∴GH:HO:OB=DE:EF:FB=1:1:2,
∴HG=HO=1,OB=2,
∴B(2,0).
∵△OBE的面积为![]() ,
,
∴![]() ×2×EH=
×2×EH=![]() ,解得EH=
,解得EH=![]() .
.
∵OF∥EH∥DG,
∴![]() =
=![]() =
=![]() ,则DG=
,则DG=![]() ×
×![]() =3,
=3,
∴D(﹣2,3).
把B(2,0),D(﹣2,3)代入y=ax2+2ax+c中,得
![]() 解得
解得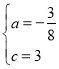
∴抛物线解析式为y=﹣![]() x2﹣
x2﹣![]() x+3 ;
x+3 ;
(2)令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() .
.
![]() ,
,
![]() .
.
设直线AC的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴直线AC的解析式为y=![]() x+3.
x+3.
过点P作PQ⊥x轴交AC于点Q,

设![]() ,则
,则![]() ,
,
![]() ,
,
即![]() ,
,
当![]() 时,
时,
解得![]() ,
,
当![]() 时,
时,
![]()
此时![]() 与
与![]() 重合,故舍去;
重合,故舍去;
当![]() 时,
时,
![]()
此时![]() .
.
当![]() 时,
时,
化简得![]() ,
,
此时![]() ,
,
∴该方程无实数根,
综上所述,点P的坐标为![]() ;
;
(3)由(2)知,![]() ,
,
又∵![]() ,
,
![]() .
.
当![]() 时,
时,
![]() ,
,
即![]() ,
,
解得![]() .
.
当![]() 时,A,B,Q三点共线,不符合题意,
时,A,B,Q三点共线,不符合题意,
∴![]() ,
,
∴∠AQB为钝角时,则m的取值范围是![]() 且
且![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
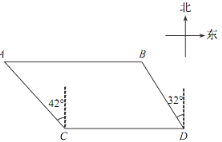
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的木栈道 AB ,栈道 AB 与景区道路CD 平行.在 C 处测得栈道一端 A 位于北偏西 42°方向,在 D 处测得栈道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木栈道 AB 的长度(结果保留整数) .
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
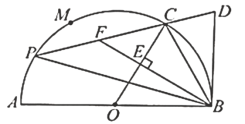
【题目】如图,![]() 为半⊙O的直径,
为半⊙O的直径,![]() ,
,![]() 是半圆上的三等分点,
是半圆上的三等分点,![]() ,
,![]() 与半⊙O相切于点
与半⊙O相切于点![]() ,点
,点![]() 为
为![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),直线
重合),直线![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,则下列结论正确的是______________.(写出所有正确结论的序号)
,则下列结论正确的是______________.(写出所有正确结论的序号)
①![]() ;②
;②![]() 的长为
的长为![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为定值.
为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=15,AC=20,tanA=![]() ,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
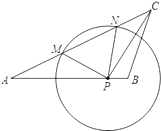
(1)求⊙P的半径;
(2)当AP=![]() 时,试探究△APM与△PCN是否相似,并说明理由.
时,试探究△APM与△PCN是否相似,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且点
轴的正半轴上,且点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交一次函数
轴的垂线,分别交一次函数![]() 的图象于点
的图象于点![]() ,交正比例函数
,交正比例函数![]() 的图象于点
的图象于点![]() .
.
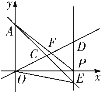
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 为何值时,
为何值时,![]() ;
;
(3)连接![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,在讨论
,在讨论![]() 的面积与
的面积与![]() 面积的大小问题时,嘉嘉认为
面积的大小问题时,嘉嘉认为![]() ,淇淇认为
,淇淇认为![]() ,请你作为小法官,帮助他们两人评判,谁的说法正确.
,请你作为小法官,帮助他们两人评判,谁的说法正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是以原点
是以原点![]() 为对称中心的矩形,
为对称中心的矩形,![]() ,
,![]() ,
,![]() 和
和![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() ,连接
,连接![]() .
.

(1)写出点![]() 和点
和点![]() 的坐标;
的坐标;
(2)求四边形![]() 的面积;
的面积;
(3)判断点![]() 在矩形
在矩形![]() 的内部还是外部;
的内部还是外部;
(4)要使直线![]() 与矩形
与矩形![]() 没有公共点,直接写出
没有公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班七个兴趣小组人数分别为4,4,5,5,x,6,7,已知这组数据的平均数是5,则这组数据的众数和中位数分别是( )
A. 4,5 B. 4,4 C. 5,4 D. 5,5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com