
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且点
轴的正半轴上,且点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交一次函数
轴的垂线,分别交一次函数![]() 的图象于点
的图象于点![]() ,交正比例函数
,交正比例函数![]() 的图象于点
的图象于点![]() .
.
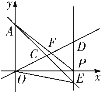
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 为何值时,
为何值时,![]() ;
;
(3)连接![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,在讨论
,在讨论![]() 的面积与
的面积与![]() 面积的大小问题时,嘉嘉认为
面积的大小问题时,嘉嘉认为![]() ,淇淇认为
,淇淇认为![]() ,请你作为小法官,帮助他们两人评判,谁的说法正确.
,请你作为小法官,帮助他们两人评判,谁的说法正确.
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】房山某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下的两个统计图.请根据下面两个不完整的统计图回答以下问题:

(1)这次抽样调查中,共调查了 名学生;
(2)补全两幅统计图;
(3)根据抽样调查的结果,估算该校1000名学生中大约有多少人选择“小组合作学习”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,过点B的直线与抛物线的另一个交点为D,与抛物线的对称轴交于点E,与y轴交于点F,且![]() ,△OBE的面积为
,△OBE的面积为![]() .
.
(1)求抛物线的解析式;
(2)设P为已知抛物线上的任意一点,当△ACP的面积等于△ACB的面积时,求点P的坐标;
(3)点Q(0,m)是y轴上的动点,连接AQ、BQ,当∠AQB为钝角时,则m的取值范围是 .(直接写出答案)
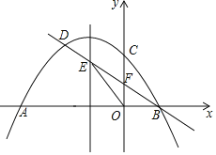
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是该直线上不同于
是该直线上不同于![]() 的点,且
的点,且![]() .
.
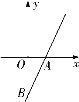
(1)写出![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)过动点![]() 且垂直于
且垂直于![]() 轴的直线与直线
轴的直线与直线![]() 交于点
交于点![]() ,若点
,若点![]() 不在线段
不在线段![]() 上,求
上,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 与直线
与直线![]() 所夹锐角为
所夹锐角为![]() ,请直接写出直线
,请直接写出直线![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣ax﹣2a(a为常数且不等于0)与x轴的交点为A,B两点,且A点在B的右侧.
(1)当抛物线经过点(3,8),求a的值;
(2)求A、B两点的坐标;
(3)若抛物线的顶点为M,且点M到x轴的距离等于AB的3倍,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“京津冀生态建设协同发展”,我区某街道要增大绿化面积,决定从备选的五种树中选一种进行栽种.为了更好的了解民意,工作人员在街道辖区范围内随机走访了部分居民,进行“我最喜欢的一种树”的调查活动(每人选其中一种树),将调查结果整理后,绘制出下面两个不完整的统计图.


请根据所给信息回答问题:
(1)这次参与调查的居民人数为________;
(2)将条形统计图补充完整;
(3)扇形统计图中,![]() ________;“白蜡”所在扇形的圆心角度数为________;
________;“白蜡”所在扇形的圆心角度数为________;
(4)已知该街道辖区内现在居民8万人,请你估计这8万人中最喜欢“银杏”的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com