
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是该直线上不同于
是该直线上不同于![]() 的点,且
的点,且![]() .
.
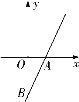
(1)写出![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)过动点![]() 且垂直于
且垂直于![]() 轴的直线与直线
轴的直线与直线![]() 交于点
交于点![]() ,若点
,若点![]() 不在线段
不在线段![]() 上,求
上,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 与直线
与直线![]() 所夹锐角为
所夹锐角为![]() ,请直接写出直线
,请直接写出直线![]() 的函数解析式.
的函数解析式.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
解:(1)对于直线![]() ,令
,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ;
;
(2)如解图①,∵点C在直线![]() 上,且
上,且![]() ,点C不与点B重合,
,点C不与点B重合,
∴点C在BA的右上方,过点C作![]() 轴于点F,
轴于点F,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,![]() ,
,
观察图象可知要使过点![]() 且垂直于x轴的直线PD与直线
且垂直于x轴的直线PD与直线![]() 的交点D不在线段BC上,则m的取值范围为:
的交点D不在线段BC上,则m的取值范围为:![]() 或
或![]() ;
;

图①
(3)直线BE的函数解析式为![]() 或
或![]()
【解法提示】如解图②,作![]() ,使得
,使得![]() ,作
,作![]() 轴于点H,则
轴于点H,则![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
设直线BE的函数解析式为![]() ,
,
将点![]() ,点
,点![]() 分别代入
分别代入
得![]() ,解得
,解得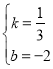 ,
,
∴直线BE的函数解析式为![]() ,
,
当直线![]() ⊥直线BE时,直线
⊥直线BE时,直线![]() 也满足条件,
也满足条件,
∴直线![]() 的函数解析式为
的函数解析式为![]() ,
,
∴满足条件的直线BE的函数解析式为![]() 或
或![]() .
.

图②
【思维教练】(1)分别令![]() ,
,![]() 求解;(2)先确定点
求解;(2)先确定点![]() 的位置,过点
的位置,过点![]() 作
作![]() 轴于点
轴于点![]() ,利用全等三角形的性质,求出点
,利用全等三角形的性质,求出点![]() 坐标即可求解;(3)直线
坐标即可求解;(3)直线![]() 位置固定,两条直线夹角为定值时,另一条直线有两种情况,且由夹角为
位置固定,两条直线夹角为定值时,另一条直线有两种情况,且由夹角为![]() ,可知两种情况下的两条直线垂直.
,可知两种情况下的两条直线垂直.


科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
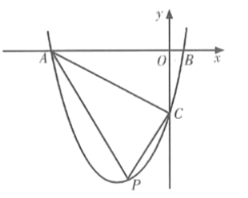
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,且
,且![]() ,点
,点![]() 是第三象限内抛物线上的一动点.
是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,点E在正方形ABCD的内部,且EB=EC,过点E画一条射线平分∠BEC;
(2)如图②,在△ABC 中,DE∥BC,EF∥AB,请仅用直尺(无刻度)作一个三角形,使所作三角形的面积等于△ABC 面积的一半并把所作的三角形用阴影表示出来.
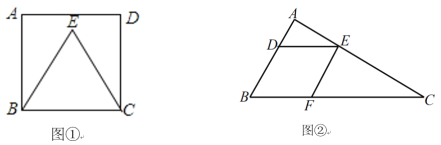
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且点
轴的正半轴上,且点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交一次函数
轴的垂线,分别交一次函数![]() 的图象于点
的图象于点![]() ,交正比例函数
,交正比例函数![]() 的图象于点
的图象于点![]() .
.
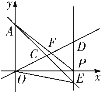
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 为何值时,
为何值时,![]() ;
;
(3)连接![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,在讨论
,在讨论![]() 的面积与
的面积与![]() 面积的大小问题时,嘉嘉认为
面积的大小问题时,嘉嘉认为![]() ,淇淇认为
,淇淇认为![]() ,请你作为小法官,帮助他们两人评判,谁的说法正确.
,请你作为小法官,帮助他们两人评判,谁的说法正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象
的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() :
:![]() 与
与![]() 轴的交点分别为
轴的交点分别为![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).

(1)当![]() 的顶点在
的顶点在![]() 上时,求
上时,求![]() 的值;
的值;
(2)若![]() 、
、![]() 两点中有一点与点
两点中有一点与点![]() 关于原点对称,试判断这个点是点
关于原点对称,试判断这个点是点![]() 还是点
还是点![]() ;
;
(3)若![]() 的顶点为
的顶点为![]() ,对称轴与
,对称轴与![]() 的交点为
的交点为![]() ,且点
,且点![]() 在点
在点![]() 的下方,当
的下方,当![]() 为何值时,线段
为何值时,线段![]() 的长最大.
的长最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
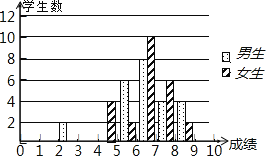
【题目】为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com