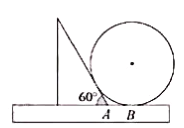
【题目】如图，一把直尺，
的直角三角板和光盘如图摆放，
为角与直尺交点，
,则光盘的直径是( )
A. 3 B. 
C. 
D. 
【答案】D
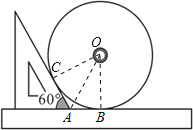
【解析】设光盘圆心为O，连接OC，OA，OB，由AC、AB都与圆O相切，利用切线长定理得到AO平分∠BAC，且OC垂直于AC，OB垂直于AB，可得出∠CAO=∠BAO=60°，得到∠AOB=30°，利用30°所对的直角边等于斜边的一半求出OA的长，再利用勾股定理求出OB的长，即可确定出光盘的直径．
如图，设光盘圆心为O，连接OC，OA，OB，
∵AC、AB都与圆O相切，
∴AO平分∠BAC，OC⊥AC，OB⊥AB，
∴∠CAO=∠BAO=60°，
∴∠AOB=30°，
在Rt△AOB中，AB=3cm，∠AOB=30°，
∴OA=6cm，
根据勾股定理得：OB=
3
，
则光盘的直径为6，
故选D.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】抛物线
经过点A（
，0），B（
，0），且与y轴相交于点C．
（1）求这条抛物线的表达式；
（2）求∠ACB的度数；
（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB为⊙O的直径，AB=4，C为半圆AB的中点，P为
上一动点，延长BP至点Q，使BPBQ=AB2．若点P由A运动到C，则点Q运动的路径长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在同一平面内，四条线AB、BC、CD、DA首尾顺次相接，AD、BC相交于点O，AM、CN分别是∠BAD和∠BCD的平分线，∠B＝α，∠D＝β．
（1）如图2，AM、CN相交于点P．
①当α＝β时，判断∠APC与α的大小关系，并说明理由．
②当α＞β时，请直接写出∠APC与α，β的数量关系．
（2）是否存在AM∥CN的情况？若存在，请判断并说明α，β的数量关系；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，反比例函数
(k≠0）与一次函数y=ax+b（a≠0）相交于点A（1，3），B（c，﹣1）．
（1）求反比例函数与一次函数的解析式；
（2）在反比例函数图象上存在点C，使△AOC为等腰三角形，这样的点有几个，请直接写出一个以AC为底边的等腰三角形顶点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利，初二数学小组在校内对“你最认可的四大新生事物”进行调查，随机调查了m人（每名学生必选一种且只能从这四种中选择一种）并将调查结果绘制成如下不完整的统计图．
（1）根据图中信息求出m= ，n= ；
（2）请你帮助他们将这两个统计图补全；
（3）根据抽样调查的结果，请估算全校2000名学生中，大约有多少人最认可“微信”这一新生事物？
（4）已知A、B两位同学都最认可“微信”，C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学，请你通过树状图或表格，求出这两位同学最认可的新生事物不一样的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠C＝90°，AC＝BC，AD＝16cm，BE＝12cm，点P是斜边AB的中点．有一把直角尺MPN，将它的顶点与点P重合，将此直角尺绕点P旋转，与两条直角边AC和CB分别交于点D和点E．则线段PD和PE的数量关系为_____，线段DE＝_____cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解市民“获取新闻的最主要途径”，某市记者开展了一次抽样调查，根据调查结果绘制了如下尚不完整的统计图．
根据以上信息解答下列问题：
（1）这次抽样调查的样本容量是 ；通过“电视”了解新闻的人数占被调查人数的百分比为 ；扇形统计图中，“手机上网”所对应的圆心角的大小是 度；
（2）请补全条形统计图；
（3）若该市约有950万人，请你估计其中有多少万人将“电脑和手机上网”作为“获取新闻的最主要途径”？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
