
����Ŀ����ͼ1����ͬһƽ���ڣ�������AB��BC��CD��DA��β˳����ӣ�AD��BC�ཻ�ڵ�O��AM��CN�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ���B��������D������

��1����ͼ2��AM��CN�ཻ�ڵ�P��
�ٵ�������ʱ���жϡ�APC�����Ĵ�С��ϵ����˵�����ɣ�
�ڵ�������ʱ����ֱ��д����APC����������������ϵ��
��2���Ƿ����AM��CN������������ڣ����жϲ�˵����������������ϵ���������ڣ���˵�����ɣ�
���𰸡���1���ٵ�������ʱ����APC���������ɼ��������ڵ�������ʱ����APC��![]() ����+������
����+������
��2�������ڣ����ɼ�����.
��������
��1���ٵ���=��ʱ�������������ڽǺͶ����á�2+��D=��4+��APC����OCD+��D=��B+��OAB�����OCD=��OAB�����ݽ�ƽ���߶���á�2=��4�����ԡ�APC=��D=�����ڡ�2+��D=��4+��APC����OCD+��D=��B+��OAB�����2+��=��4+��APC��2��2+��=��+2��4�����ԡ�APC=![]() ����+������
����+������
��2����AM��CN�����4=��5���ɡ�5=��2+��D�õ���4=��2+����ͬ���á�3=��1+����Ȼ�������ʽ��ӵõ���+��=0���ɴ��жϲ�����AM��CN��
��1����ͼ2��
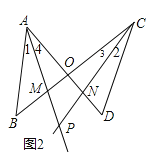
�ٵ�������ʱ����APC�������������£�
����ANP����CND����2+��D����4+��APC��
����AOB����COD����OCD+��D����B+��OAB��
�ߡ�D����B������
���OCD����OAB��
��AM��CN�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ�
���OCD��2��2����OAB��2��4��
���2����4��
���APC����D������
�ڵ�������ʱ����APC��![]() ����+������
����+������
�ߡ�2+��D=��4+��APC����OCD+��D=��B+��OAB��
���2+��=��4+��APC��2��2+��=��+2��4��
���APC=��2-��4+������2-��4=![]() ��-
��-![]() ��
��
���APC=![]() ��-
��-![]() ��+��=
��+��=![]() ��+
��+![]() ����
����
���ԡ�APC=![]() ����+������
����+������
��2�������ڣ��������£�
��ͼ1��
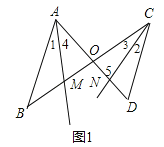
��AM��CN�����4����5��
�ߡ�5����2+��D��
���4����2+����
ͬ���á�3����1+��B������3����1+����
���3+��4����1+��2+��+����
��AM��CN�ֱ��ǡ�BAD�͡�BCD��ƽ���ߣ�
���3����2����1����4��
����+����0��
�����AM��CN��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͥ����ҩƷ����������Σ�շ�����������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ���˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������飮
��Ƶ��鷽ʽ��
��1��������ѡȡ�����ķ���
����������ij���������Լ�ͥΪ��λ�����ȡ
����ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ
����ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
�����������һ������ ������ֻ��������ȷ�𰸵���ţ�
�ռ��������ݣ�
���γ������鷢�֣����ܵ���ļ�ͥ���й���ҩƷ���ֽ��й����ݳ������±���
���� ��ʽ | A ����ʹ�� | B ֱ�Ӷ��� | C �ͻ��յ� | D ���ü��� | E ����ҩ�� | F ֱ�ӷ��� |
��ռ���� | 8% | 51% | 10% | 20% | 6% | 5% |
�������ݣ�
��2���˴γ�����������Ϊ1000����ͥ�������������ͳ��ͼ�������ִ�������ҩƷ��ʽ�ļ�ͥ����

�������ݣ�
��3�����ݵ������ݣ�����Ϊ���������ͥ��������ҩƷ����ķ�ʽ��ʲô��˵��������ɣ�
��4����ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������500��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ͼ1Ϊ������ֽƬABC����P��AB�ϣ�����ֽƬ�����۵�����ͼ2��ʾ����A��B��Cǡ���غ��ڵ�P�����ۺ۷ֱ�ΪSR��RQ��QT���ۺ۵Ľ���R��Q�ֱ��ڱ�AC��BC�ϣ�����ABC���ı���PTQR������ֱ���20��7������RPS�������_____��
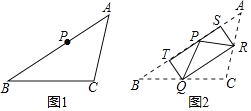
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߲�Ʒ�ĸ���ֵ��ij��˾�ƻ����з�������1200���²�Ʒ���о��ӹ�����Ͷ���г������мס��������������߱��ӹ���������˾�ɳ������Ա�ֱ������������˽���������������Ϣ��
��Ϣһ�����������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ����10�죻
��Ϣ�����ҹ���ÿ��ӹ��������Ǽ���ÿ��ӹ�������1.5����
����������Ϣ����ס�����������ÿ��ֱ��ܼӹ����ټ��²�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A��20������ABC���ACB��ƽ���߽��ڵ�D1����ABD1���ACD1��ƽ���߽��ڵ�D2���Դ����ƣ���ABD2���ACD2��ƽ���߽��ڵ�D�����BDC�Ķ�����__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�͡�DEF�У���ACB=��EFD=90�㣬��B��F��C��D��ͬһֱ���ϣ���֪AB��DE����AB=DE��AC=6��EF=8��DB=10����CF�ij���Ϊ___________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
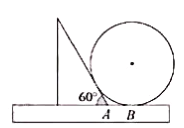
����Ŀ����ͼ��һ��ֱ�ߣ�![]() ��ֱ�����ǰ������ͼ�ڷţ�
��ֱ�����ǰ������ͼ�ڷţ�![]() Ϊ
Ϊ![]() ����ֱ�߽��㣬
����ֱ�߽��㣬![]() ,����̵�ֱ����( )
,����̵�ֱ����( )
A. 3 B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ɽ�ǹ���5A���羰����������һ�����㱻��Ϊ����һ�ҩ����������ң��������ұڻ��߶ȴ�ʯ��F����ʼһֱ��ֱ��ɽ��E����Ϊ�˲������������ϱڻ��ĸ߶ȣ�С����ɽ��A�������¶�i=0.75��б������65����C������C�����ɽ��E������Ϊ26.5����������ǰ��ˮƽ��15����D������D����ñڻ���F���ĸ���Ϊ42�����ڻ���F������ɽ��B���ľ�����12�ף�A��B��C��D��E��F��ͬһƽ���ڣ�A��B��ͬһˮƽ���ϣ�EB��AB������С���IJ������ݣ���ڻ��ĸ߶�EFΪ���������ף���ȷ��0.1�ף��ο����ݣ�sin26.5���0.45��cos26.5���0.9��tan26.5���0.5��sin42���0.67��cos42���0.74��tan42���0.9��

A. 49.5 B. 68.7 C. 69.7 D. 70.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCO�����Ϊ15����OA��OC��2��EΪBC���е㣬��OEΪֱ������O����![]() ����D�㣬����D��DF��AE�ڵ�F��
����D�㣬����D��DF��AE�ڵ�F��

��1����OA��OC�ij���
��2����֤��DFΪ��O�������ߣ�
��3��С���ڽ����ʱ��������AOE�ǵ��������Ρ��ɴˣ����϶�����ֱ��BC��һ�����ڳ���E����ĵ�P��ʹ��AOPҲ�ǵ��������Σ��ҵ�Pһ������O����������ͬ�����Ŀ���������˵�����ɡ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com