练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC和△DEF中，∠ACB=∠EFD=90°，点B、F、C、D在同一直线上，已知AB⊥DE，且AB=DE，AC=6，EF=8，DB=10，则CF的长度为___________.

    【答案】4

    【解析】

    先利用AAS证明△ABC≌△DEF，根据全等三角形的性质可得DF=AC=6，BC=EF=8，继而根据线段的和差进行求解即可得.

    ∵AC⊥BD，EF⊥BD，DE⊥AB，

    ∴∠ACB=∠ACD=90°，∠EFD=90°，∠3=90°，

    ∴∠ACB=∠EFD，∠1+∠A=90°，∠2+∠D=90°，

    又∵∠1=∠2，

    ∴∠A=∠D，

    又∵AB=DE，

    ∴△ABC≌△DEF(AAS)，

    ∴DF=AC=6，BC=EF=8，

    ∴CD=BD-BC=10-8=2，

    ∴CF=DF-CD=6-2=4，

    故答案为：4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知点A（x1，y1）、B（x2，y2）在二次函数y=x2+mx+n的图象上，当x1=1、x2=3时，y1=y2．

    （1）①求m；②若抛物线与x轴只有一个公共点，求n的值．

    （2）若P（a，b1），Q（3，b2）是函数图象上的两点，且b1＞b2，求实数a的取值范围．

    （3）若对于任意实数x1、x2都有y1+y2≥2，求n的范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC 中，AD 是 BC 边上的中线．

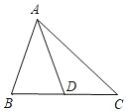
    （1）画出与△ACD 关于点 D 成中心对称的三角形；

    （2）找出与 AC 相等的线段；

    （3）探索：△ABC 中，AB+AC 与中线 AD 之间的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AOB=20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记∠MPQ=，∠PQN=，当MP+PQ+QN最小时，则的值为( )

    A. 10°B. 20°C. 40°D. 60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读并解决问题：有趣的勾股数组

    定义：一般地，若三角形三边长，，都是正整数，且满足，那么数组称为勾股数组．

    关于勾股数组的研究我国历史上有过非常辉煌的成就，根据我国古代数学书《周髀算经》记载，在约公元前1100年，人们就已经知道“勾广三，股修四，径隅五”（古人把较短的直角边称为勾，较长直角边称为股，而斜边则成称为弦），即知道了勾股数组，后来人们发现并证明了勾股定理．

    公元263年魏朝刘徽注《九章算术》，文中除提到勾股数组以外，还提到，，，等勾股数组．

    设，是两个正整数，且，三角形三边长，，都是正整数．

    下表中的，，可以组成一些有规律的勾股数组：

    2

    1

    3

    4

    5

    3

    2

    5

    12

    13

    4

    1

    15

    8

    17

    4

    3

    7

    24

    25

    5

    2

    21

    20

    29

    5

    4

    9

    40

    41

    6

    1

    35

    12

    37

    6

    5

    11

    60

    61

    7

    2

    45

    28

    53

    7

    4

    33

    56

    65

    7

    6

    13

    84

    85

    请你仔细观察这个表格，解答下列问题：

    （1）表中和，的等量关系式是________；

    （2）表中的勾股数组用只含，的代数式表示为________；

    （3）小明通过研究表中数据发现：若勾股数组中，弦与股的差为1，则勾股数的形式可表述为（，为正整数），请你用含的代数式表示．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，点在上，平分，且，连接并延长与的延长线交于点，连接，若，则面积是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC和△ABD中，∠BAC=∠ABD=90°，点E为AD边上的一点，且AC=AE，连接CE交AB于点G，过点A作AF⊥AD交CE于点F.

    (1)求证：△AGE≌△AFC；

    (2)若AB=AC，求证：AD=AF+BD.

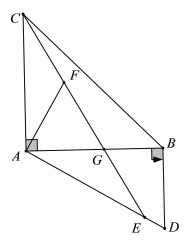
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】终身学习是学习型社会的核心内容，努力建设“学习型家庭”也是一个重要组成部分．为了解“学习型家庭”情况，某社区对部分家庭六月份的平均每天看书学习时间进行了一次抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图，请根据图中提供的信息，解答下列问题：

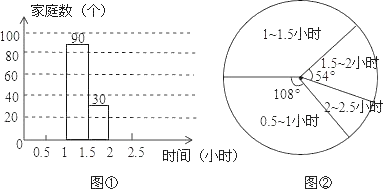
    （1）本次抽样调查了多少个家庭；

    （2）将图①中的条形图补充完整；

    （3）学习时间在1～1.5小时的部分对应的扇形圆心角的度数是多少；

    （4）若该社区有家庭有5000个，请你估计该社区学习时间不少于1小时的约有多少个家庭？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O是正△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB=150°；④S四边形AOBO；⑤S△AOC+S△AOB=．其中正确的结论是（　　）

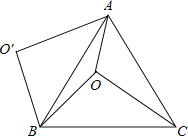
    A.①②③⑤B.①②③④C.①②③④⑤D.①②③

    查看答案和解析>>

    同步练习册答案