
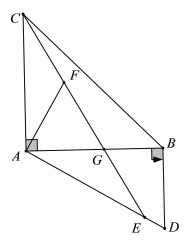
【题目】如图,在△ABC和△ABD中,∠BAC=∠ABD=90°,点E为AD边上的一点,且AC=AE,连接CE交AB于点G,过点A作AF⊥AD交CE于点F.
(1)求证:△AGE≌△AFC;
(2)若AB=AC,求证:AD=AF+BD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由AF⊥AD,∠CAB=90°,可得∠CAF=∠EAG,由AC=AE,可得∠ACF=∠AEG,根据AAS即可证明结论;
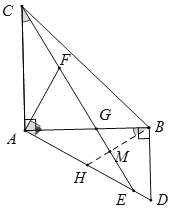
(2)如图,在AD上截取AH=AE,交CE于点M,证明△CAF≌△BAH,从而可得∠ABH=∠ACF,继而可得∠MGB+∠ABH=90°,从而可得∠MHE+∠HEM=90°,再根据∠ACF=∠HEM,∠ABH+∠HBD=90°,可得到∠MHE=∠HBD,从而可得HD=BD,再根据AD=AH+DH,即可求得答案.
(1)∵AF⊥AD,
∴∠FAE=90°,
∵∠CAB=90°,
∴∠CAB-∠FAB=∠FAE-∠FAB,
即∠CAF=∠EAG,
∵AC=AE,
∴∠ACF=∠AEG,
∴△AGE≌△AFC(AAS);
(2)如图,在AD上截取AH=AE,交CE于点M,
又∵∠CAF=∠BAH,AC=BC,
∴△CAF≌△BAH(SAS),
∴∠ABH=∠ACF,
∵∠CGA=∠MGB,∠ACF+∠CGA=90°,
∴∠MGB+∠ABH=90°,
∴∠BMG=90°,
∴∠HME=∠BMG=90°,
∴∠MHE+∠HEM=90°,
又∵∠ACF=∠HEM,∠ABH+∠HBD=90°,
∴∠MHE=∠HBD,
∴HD=BD,
∵AD=AH+DH,
∴AD=AF+BD.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△AOB是等边三角形,且B(2,0),OC是AB边的中线,将△AOB绕点O逆时针旋转120°得到△A1OB1.
(1)B1的坐标是_______(直接写出结果即可);
(2)请画出将△A1OB1绕点O逆时针旋转120°得到的△A2OB2,并按图形旋转规律画出阴影部分;
(3)计算点B旋转到点B1所经过的弧形路线长(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
(1)求证:CP为⊙O的切线;
(2)若BP=1,CP=![]() ,求 ⊙O的半径;
,求 ⊙O的半径;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,∠ACB=∠EFD=90°,点B、F、C、D在同一直线上,已知AB⊥DE,且AB=DE,AC=6,EF=8,DB=10,则CF的长度为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、2、3、4.
(1)搅匀后从中任意摸出1个球,求摸出的乒乓球球面上数字为1的概率;
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,求2次摸出的乒乓球球面上数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一平面中,两条直线相交有一个交点;三条直线两两相交最多有3个交点;四条直线两两相交最多有6个交点……当相交直线的条数从2至n变化时,最多可有的交点数m与直线条数n之间的关系如下表:

则m与n的关系式为:___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种商品,若购进A种商品2件和B种商品1件需45元;若购进A种商品3件和B种商品2件需70元.
(1)A、B两种商品每件的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过1000元,最多能购进A种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
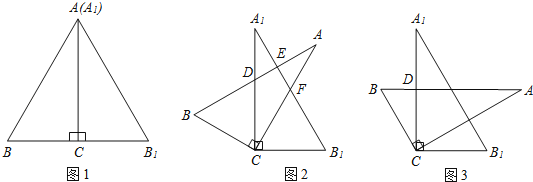
【题目】将两块全等的含30°角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.
(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
①填空:当旋转角等于20°时,∠BCB1= 度;
②当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
(2)将图2中的三角板ABC绕点C顺时针方向旋转至图3的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com