
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
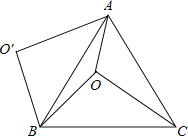
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
【答案】A
【解析】
证明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC绕点B逆时针旋转60°得到,故结论①正确;由△OBO′是等边三角形,可知结论②正确;在△AOO′中,三边长为3,4,5,这是一组勾股数,故△AOO′是直角三角形;进而求得∠AOB=150°,故结论③正确;S四边形AOBO=S△AOO+S△OBO,可得结论④错误;如图②,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.利用旋转变换构造等边三角形与直角三角形,将S△AOC+S△AOB转化为S△COO+S△AOO,计算可得结论⑤正确.
由题意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,
又∵OB=O′B,AB=BC,
∴△BO′A≌△BOC,又∵∠OBO′=60°,
∴△BO′A可以由△BOC绕点B逆时针旋转60°得到,
故结论①正确;
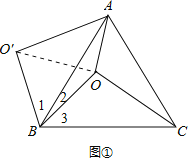
如图①,连接OO′,
∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等边三角形,
∴OO′=OB=4.
故结论②正确;
∵△BO′A≌△BOC,∴O′A=5.
在△AOO′中,三边长为3,4,5,这是一组勾股数,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故结论③正确;
S四边形AOBO′=S△AOO′+S△OBO′=![]() ,
,
故结论④错误;
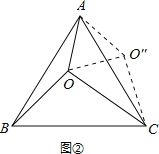
如图②所示,将△AOB绕点A逆时针旋转60°,使得AB与AC重合,点O旋转至O″点.
易知△AOO″是边长为3的等边三角形,△COO″是边长为3、4、5的直角三角形,
则S△AOC+S△AOB=S四边形AOCO″=S△COO″+S△AOO″=![]() ,
,
故结论⑤正确.
综上所述,正确的结论为:①②③⑤.
故选A.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,∠ACB=∠EFD=90°,点B、F、C、D在同一直线上,已知AB⊥DE,且AB=DE,AC=6,EF=8,DB=10,则CF的长度为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种商品,若购进A种商品2件和B种商品1件需45元;若购进A种商品3件和B种商品2件需70元.
(1)A、B两种商品每件的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过1000元,最多能购进A种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金是x元,发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆,已知所有观光车每天的管理费是1000元.
(1)若某日的净收入为5000元,且使游客得到实惠,则当天的观光车的日租金是多少元?(注:净收入=租车收入-管理费)
(2)设每日净收入为w元,请写出w与x之间的函数关系式;并求出日租金为多少时,每日净收入最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
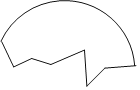
【题目】考古学家发现了一块古代圆形陶器残片如图所示,为了修复这块陶器残片,需要找出圆心.
(1)请利用尺规作图确定这块残片的圆心O;(保留作图痕迹,不写作法)
(2)写出作图的主要依据:_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
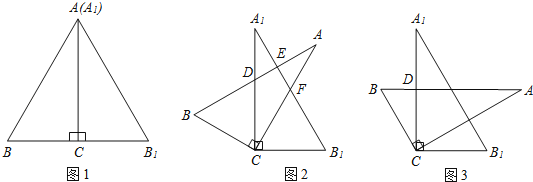
【题目】将两块全等的含30°角的直角三角板按图1的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.
(1)固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图2的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
①填空:当旋转角等于20°时,∠BCB1= 度;
②当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
(2)将图2中的三角板ABC绕点C顺时针方向旋转至图3的位置,使AB∥CB1,AB与A1C交于点D,试说明A1D=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某品牌的饮料有大瓶与小瓶装之分.某超市花了2100元购进一批该品牌的饮料共800瓶,其中,大瓶和小瓶饮料的进价及售价如右表所示.
大瓶 | 小瓶 | |
进价(元/瓶) |
|
|
售价(元/瓶) |
|
|
(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润为1075元,那么小瓶饮料作为赠品送出多少瓶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com