
【题目】如图,在![]() 中,点
中,点![]() 在
在![]() 上,
上,![]() 平分
平分![]() ,且
,且![]() ,连接
,连接![]() 并延长与
并延长与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 面积是________.
面积是________.
【答案】![]()
【解析】
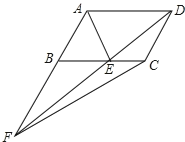
由平行四边形的性质和角平分线的定义得出∠BAE=∠BEA,得出AB=BE=AE,所以△ABE是等边三角形,由AB的长,可求出△ABE的面积,再根据△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),可得S△FCD=S△ABC,又因为△AEC与△DEC同底等高,所以S△AEC=S△DEC,即S△ABE=S△CEF问题得解.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形,
∵AB=4,
∴△ABE的面积=![]() ,
,
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△FCD-S△DEC=S△ABC-S△AEC,
∴S△ABE=S△CEF=![]() .
.
故答案为:![]() .
.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
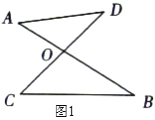
【题目】如图1,在平面直角坐标系中,已知点A(0,a),B(0,b)在y轴上,点 C(m,b)是第四象限内一点,且满足![]() ,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.
,△ABC的面积是56;AC交x轴于点D,E是y轴负半轴上的一个动点.
(1)求C点坐标;
(2)如图2,连接DE,若DE![]() AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;
AC于D点,EF为∠AED的平分线,交x轴于H点,且∠DFE=90°,求证:FD平分∠ADO;
(3)如图3,E在y轴负半轴上运动时,连EC,点P为AC延长线上一点,EM平分 ∠AEC,且PM⊥EM于M点,PN⊥x轴于N点,PQ平分∠APN,交x轴于Q点,则E在运动过程中,![]() 的大小是否发生变化,若不变,求出其值;若变化,请说明理由.
的大小是否发生变化,若不变,求出其值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,线段
,线段![]() 、
、![]() 相交于
相交于![]() ,连结
,连结![]() 、
、![]() ,我们把形如图
,我们把形如图![]() 的图形称之为“
的图形称之为“![]() ”字形,如图
”字形,如图![]() ,在图
,在图![]() 的条件下,
的条件下,![]() 和
和![]() 的平分线
的平分线![]() 和
和![]() 相交于点
相交于点![]() ,并且与
,并且与![]() 、
、![]() 分别相交于
分别相交于![]() 、
、![]() ,试解答下列问题:
,试解答下列问题:
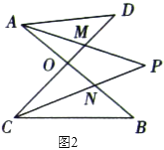
(1)在图![]() 中,请直接写出
中,请直接写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系:__________
之间的数量关系:__________
(2)仔细观察,在图![]() 中“
中“![]() ”字形的个数:______个;
”字形的个数:______个;
(3)图![]() 中,当
中,当![]() 度,
度,![]() 度时,求
度时,求![]() 的度数.
的度数.
(4)图![]() 中
中![]() 和
和![]() 为任意角时,其它条件不变,试问
为任意角时,其它条件不变,试问![]() 与
与![]() 、
、![]() 之间存在着怎样的数量关系?(直接写出结果,不必证明)
之间存在着怎样的数量关系?(直接写出结果,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.

(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,∠ACB=∠EFD=90°,点B、F、C、D在同一直线上,已知AB⊥DE,且AB=DE,AC=6,EF=8,DB=10,则CF的长度为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
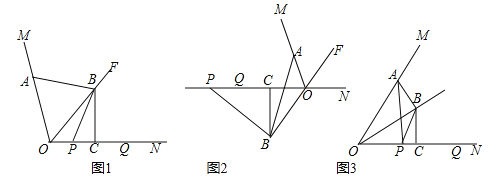
【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF、ON交于点B、点C,连接AB、PB.
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设![]() =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
【答案】(1)AB=PB;(2)存在;(3)k=0.5.
【解析】试题分析:(1)结论:AB=PB.连接BQ,只要证明△AOB≌△PQB即可解决问题;
(2)存在.证明方法类似(1);
(3)连接BQ.只要证明△ABP∽△OBQ,即可推出![]() =
=![]() ,由∠AOB=30°,推出当BA⊥OM时,
,由∠AOB=30°,推出当BA⊥OM时, ![]() 的值最小,最小值为0.5,由此即可解决问题;
的值最小,最小值为0.5,由此即可解决问题;
试题解析:解:(1)连接:AB=PB.理由:如图1中,连接BQ.

∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∴∠AOB=∠BQO,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(2)存在,理由:如图2中,连接BQ.
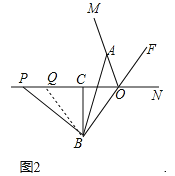
∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∠BOQ=∠FON,∴∠AOF=∠FON=∠BQC,∴∠BQP=∠AOB,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(3)连接BQ.
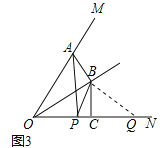
易证△ABO≌△PBQ,∴∠OAB=∠BPQ,AB=PB,∵∠OPB+∠BPQ=180°,∴∠OAB+∠OPB=180°,∠AOP+∠ABP=180°,∵∠MON=60°,∴∠ABP=120°,∵BA=BP,∴∠BAP=∠BPA=30°,∵BO=BQ,∴∠BOQ=∠BQO=30°,∴△ABP∽△OBQ,∴ ![]() =
=![]() ,∵∠AOB=30°,∴当BA⊥OM时,
,∵∠AOB=30°,∴当BA⊥OM时, ![]() 的值最小,最小值为0.5,∴k=0.5.
的值最小,最小值为0.5,∴k=0.5.
点睛:本题考查相似综合题、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.
【题型】解答题
【结束】
28
【题目】如图,已知抛物线y=ax2+![]() x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣![]() x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.

(1)试求该抛物线表达式;
(2)如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;
(3)如图(2),过点P作PH⊥y轴,垂足为H,连接AC.
①求证:△ACD是直角三角形;
②试问当P点横坐标为何值时,使得以点P、C、H为顶点的三角形与△ACD相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
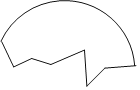
【题目】考古学家发现了一块古代圆形陶器残片如图所示,为了修复这块陶器残片,需要找出圆心.
(1)请利用尺规作图确定这块残片的圆心O;(保留作图痕迹,不写作法)
(2)写出作图的主要依据:_______________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com