
ЁОЬтФПЁПШчЭМ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЁЂ
ЁЂ![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌСЌНс
ЃЌСЌНс![]() ЁЂ
ЁЂ![]() ЃЌЮвУЧАбаЮШчЭМ
ЃЌЮвУЧАбаЮШчЭМ![]() ЕФЭМаЮГЦжЎЮЊЁА
ЕФЭМаЮГЦжЎЮЊЁА![]() ЁБзжаЮЃЌШчЭМ
ЁБзжаЮЃЌШчЭМ![]() ЃЌдкЭМ
ЃЌдкЭМ![]() ЕФЬѕМўЯТЃЌ
ЕФЬѕМўЯТЃЌ![]() КЭ
КЭ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() КЭ
КЭ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌВЂЧвгы
ЃЌВЂЧвгы![]() ЁЂ
ЁЂ![]() ЗжБ№ЯрНЛгк
ЗжБ№ЯрНЛгк![]() ЁЂ
ЁЂ![]() ЃЌЪдНтД№ЯТСаЮЪЬтЃК
ЃЌЪдНтД№ЯТСаЮЪЬтЃК
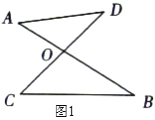
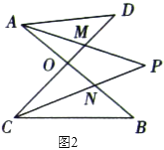
(1)дкЭМ![]() жаЃЌЧыжБНгаДГі
жаЃЌЧыжБНгаДГі![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() жЎМфЕФЪ§СПЙиЯЕЃК__________
жЎМфЕФЪ§СПЙиЯЕЃК__________
(2)заЯИЙлВьЃЌдкЭМ![]() жаЁА
жаЁА![]() ЁБзжаЮЕФИіЪ§ЃК______ИіЃЛ
ЁБзжаЮЕФИіЪ§ЃК______ИіЃЛ
(3)ЭМ![]() жаЃЌЕБ
жаЃЌЕБ![]() ЖШЃЌ
ЖШЃЌ![]() ЖШЪБЃЌЧѓ
ЖШЪБЃЌЧѓ![]() ЕФЖШЪ§.
ЕФЖШЪ§.
(4)ЭМ![]() жа
жа![]() КЭ
КЭ![]() ЮЊШЮвтНЧЪБЃЌЦфЫќЬѕМўВЛБфЃЌЪдЮЪ
ЮЊШЮвтНЧЪБЃЌЦфЫќЬѕМўВЛБфЃЌЪдЮЪ![]() гы
гы![]() ЁЂ
ЁЂ![]() жЎМфДцдкзХдѕбљЕФЪ§СПЙиЯЕЃП(жБНгаДГіНсЙћЃЌВЛБижЄУї)
жЎМфДцдкзХдѕбљЕФЪ§СПЙиЯЕЃП(жБНгаДГіНсЙћЃЌВЛБижЄУї)
ЁОД№АИЁП(1)![]() ЃЛ(2)6ЃЛ(3)
ЃЛ(2)6ЃЛ(3)![]() ЃЛ(4)
ЃЛ(4)![]() .
.
ЁОНтЮіЁП
(1)ИљОнШ§НЧаЮЕФФкНЧКЭЖЈРэвдМАЖдЖЅНЧЯрЕШСаЪНећРэМДПЩЕУНтЃЛ
(2)ИљОнЖЅЕуевГіЁА8зжаЮЁБЕФИіЪ§МДПЩЃЛ
(3)ИљОнНЧЦНЗжЯпЕФЖЈвхПЩЕУЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯ4ЃЌИљОнЁА![]() зжаЮЁБаджЪПЩЕУЃК
зжаЮЁБаджЪПЩЕУЃК![]() ЂйЃЌ
ЂйЃЌ![]() ЂкЃЌМЬЖјПЩЕУ
ЂкЃЌМЬЖјПЩЕУ![]() ЃЌДњШыЯрЙиЪ§ОнМДПЩЧѓЕУД№АИЃЛ
ЃЌДњШыЯрЙиЪ§ОнМДПЩЧѓЕУД№АИЃЛ
(4)ИљОн(3)ЕФЭЦЕМЗНЗЈМДПЩЧѓЕУНсТл.
(1)ИљОнШ§НЧаЮЕФФкНЧКЭЖЈРэЃЌЁЯAOD+ЁЯA+ЁЯD=180ЁуЃЌЁЯBOC+ЁЯB+ЁЯC=180ЁуЃЌ
ЁпЁЯAOD=ЁЯBOC(ЖдЖЅНЧЯрЕШ)ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃКЁЯA+ЁЯD=ЁЯB+ЁЯCЃЛ
(2) вдЕуOЮЊЖЅЕуЕФЁА8зжаЮЁБгаЁїAODКЭЁїBOCЃЌЁїAOMКЭЁїCONЃЌЁїAODКЭЁїCONЃЌЁїAOMКЭЁїBOCЃЌ
вдЕуMЮЊЖЅЕуЕФЁА8зжаЮЁБгаЁїADMКЭЁїCMPЃЌ
вдЕуNЮЊЖЅЕуЕФЁА8зжаЮЁБгаЁїANPКЭЁїBCNЃЌ
ЙВга6ИіЃЌ
ЙЪД№АИЮЊЃК6ЃЛ
(3)ШчЭМ2ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ
ЁрЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯ4ЃЌ
ИљОнЁА![]() зжаЮЁБаджЪПЩЕУЃК
зжаЮЁБаджЪПЩЕУЃК
![]() ЂйЃЌ
ЂйЃЌ
![]() ЂкЃЌ
ЂкЃЌ
гЩЂй![]() ЂкЕУЃЌ
ЂкЕУЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
гж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЛ
ЃЛ
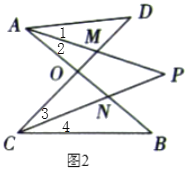
(4)![]() ЃЌРэгЩШчЯТЃК
ЃЌРэгЩШчЯТЃК
ШчЭМ2ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ
ЁрЁЯ1=ЁЯ2ЃЌЁЯ3=ЁЯ4ЃЌ
ИљОнЁА![]() зжаЮЁБаджЪПЩЕУЃК
зжаЮЁБаджЪПЩЕУЃК
![]() ЂйЃЌ
ЂйЃЌ
![]() ЂкЃЌ
ЂкЃЌ
гЩЂй![]() ЂкЕУЃЌ
ЂкЕУЃЌ
![]() ЃЌ
ЃЌ
МД![]() .
.


 ФмСІЦРМлЯЕСаД№АИ
ФмСІЦРМлЯЕСаД№АИ ЬЦгЁЮФЛЏПЮЪБВтЦРЯЕСаД№АИ
ЬЦгЁЮФЛЏПЮЪБВтЦРЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯп![]() ЁЮ
ЁЮ![]() ЃЌвЛдВНЛжБЯпaЃЌbЗжБ№гкAЁЂBЁЂCЁЂDЫФЕуЃЌЕуPЪЧдВЩЯЕФвЛИіЖЏЕуЃЌСЌНгPAЁЂPC.
ЃЌвЛдВНЛжБЯпaЃЌbЗжБ№гкAЁЂBЁЂCЁЂDЫФЕуЃЌЕуPЪЧдВЩЯЕФвЛИіЖЏЕуЃЌСЌНгPAЁЂPC.
(1)ШчЭМ1ЃЌжБНгаДГіЁЯPABЁЂЁЯPCDЁЂЁЯPжЎМфЕФЪ§СПЙиЯЕЮЊЁЁ ЁЁ ЃЛ
(2)ШчЭМ2ЃЌжБНгаДГіЁЯPABЁЂЁЯPCDЁЂЁЯPжЎМфЕФЪ§СПЙиЯЕЮЊЁЁ ЁЁ
(3)ШчЭМ3ЃЌЧѓжЄЃКЁЯPЃНЁЯPAB+ЁЯPCDЃЛ
(4)ШчЭМ4ЃЌжБНгаДГіЁЯPABЁЂЁЯPCDЁЂЁЯPжЎМфЕФЪ§СПЙиЯЕЮЊ ЁЁ ЁЁ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇзМБИАсШыаТаЃЩс,дкЧЈШыаТаЃЩсЧАОЭИУаЃ300УћбЇЩњШчКЮЕНаЃЮЪЬтНјааСЫвЛДЮЕїВщ,ВЂЕУЕНШчЯТЪ§Он:
ВНаа | 65ШЫ |
ЦяздааГЕ | 100ШЫ |
зјЙЋЙВЦћГЕ | 125ШЫ |
ЦфЫћ | 10ШЫ |
ЁЁЁЁ
НЋЩЯУцЕФЪ§ОнЗжБ№жЦГЩЩШаЮЭГМЦЭМКЭЬѕаЮЭГМЦЭМ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ ![]() ЃЌCDЪЧаББпABЩЯЕФИп.
ЃЌCDЪЧаББпABЩЯЕФИп.
(1)жЄУї: ![]() Ёз
Ёз![]()
(2)аДГіГ§(1)ЭтЕФСэСНЖдЯрЫЦШ§НЧаЮ.
(3)ACЪЧФФСНЬѕЯпЖЮЕФБШР§жаЯю?ЧыМђвЊжЄУї(ЫЕУї).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
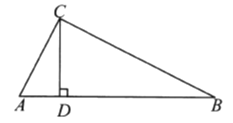
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЁїABC жаЃЌAD ЪЧ BC БпЩЯЕФжаЯпЃЎ
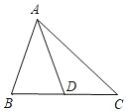
ЃЈ1ЃЉЛГігыЁїACD ЙигкЕу D ГЩжааФЖдГЦЕФШ§НЧаЮЃЛ
ЃЈ2ЃЉевГігы AC ЯрЕШЕФЯпЖЮЃЛ
ЃЈ3ЃЉЬНЫїЃКЁїABC жаЃЌAB+AC гыжаЯп AD жЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉНтЗНГЬЃК 3yЃЈyЉ1ЃЉ=2Љ2y
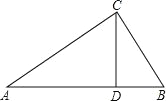
ЃЈ2ЃЉШчЭМЃЌЁїABCжаЃЌCDЪЧБпABЩЯЕФИпЃЌЧв![]() ЃЎЧѓЁЯACBЕФДѓаЁЃЎ
ЃЎЧѓЁЯACBЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯAOB=20ЁуЃЌЕуMЁЂNЗжБ№ЪЧБпOAЁЂOBЩЯЕФЖЈЕуЃЌЕуPЁЂQЗжБ№ЪЧБпOBЁЂOAЩЯЕФЖЏЕуЃЌМЧЁЯMPQ=![]() ЃЌЁЯPQN=
ЃЌЁЯPQN=![]() ЃЌЕБMP+PQ+QNзюаЁЪБЃЌдђ
ЃЌЕБMP+PQ+QNзюаЁЪБЃЌдђ![]() ЕФжЕЮЊ( )
ЕФжЕЮЊ( )

A. 10ЁуB. 20ЁуC. 40ЁуD. 60Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
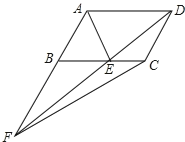
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌЕу
жаЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄгы
ВЂбгГЄгы![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() УцЛ§ЪЧ________ЃЎ
УцЛ§ЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌPЪЧCDБпЩЯвЛЕуЃЌЧвAPКЭBPЗжБ№ЦНЗжЁЯDABКЭЁЯCBAЃЌШєAD=5ЃЌAP=8ЃЌдђЁїAPBЕФжмГЄЪЧ ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com