
【题目】(1)解方程: 3y(y﹣1)=2﹣2y
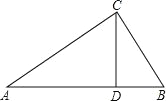
(2)如图,△ABC中,CD是边AB上的高,且![]() .求∠ACB的大小.
.求∠ACB的大小.
【答案】(1)![]() ,y2=1;(2) 90°.
,y2=1;(2) 90°.
【解析】试题分析:
(1)根据本题特点,用“因式分解法”解此方程即可;
(2)由△ABC中,CD是边AB上的高,可得∠ADC=∠CDB=90°,结合![]() 可证得:△ADC∽△CDB,从而可得∠BCD=∠A,结合∠A+∠ACD=90°可得∠BCD+∠ACD=∠ACB=90°.
可证得:△ADC∽△CDB,从而可得∠BCD=∠A,结合∠A+∠ACD=90°可得∠BCD+∠ACD=∠ACB=90°.
试题解析:
(1)方程整理得:3y(y-1)-2(y-1)=0,
分解因式得:(3y-2)(y-1)=0,
解得: ![]() ,y2=1.
,y2=1.
(2)∴∠ADC=∠BDC=90°;
又∵AD:CD=CD:BD,
∴△ADC∽△CDB;
∴∠ACD=∠B;
∵∠A+∠ACD=90°,
∴∠A+∠B=90°,即∠ACB=90°.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:

(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)条件下,哪种方案获利最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在购买某场足球门票时,设购买门票数为x(张),费用为y(元).现有两种购买方案:
方案一:若单位费助广告费10000元,则该单位所购门票的价格为每张60元;(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示.
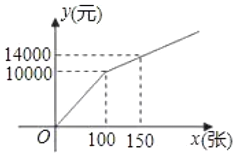
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0![]() x
x![]() 100时,y与x的函数关系式为 ;
100时,y与x的函数关系式为 ;
当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD,AB=4,BC=![]() .
.
(1)直接写出:∠ABD=______度;
(2)将矩形ABCD沿BD剪开得到两个三角形,按图2摆放:点A与点C重合,CD落在AD′上,直接写出BD与B′D′的关系:_____;
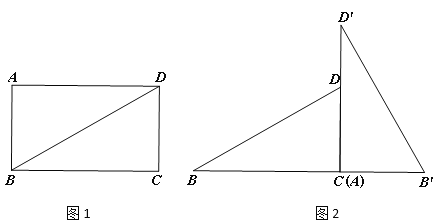
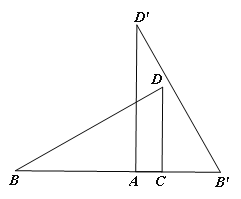
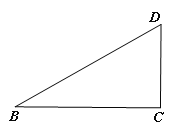
(3)在图2的基础上将△AB′D′向左平移,点B′与B重合停止,设AC=x,两个三角形重合部分的封闭图形的周长为y,请用x表示y:____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,线段
,线段![]() 、
、![]() 相交于
相交于![]() ,连结
,连结![]() 、
、![]() ,我们把形如图
,我们把形如图![]() 的图形称之为“
的图形称之为“![]() ”字形,如图
”字形,如图![]() ,在图
,在图![]() 的条件下,
的条件下,![]() 和
和![]() 的平分线
的平分线![]() 和
和![]() 相交于点
相交于点![]() ,并且与
,并且与![]() 、
、![]() 分别相交于
分别相交于![]() 、
、![]() ,试解答下列问题:
,试解答下列问题:
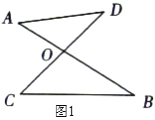
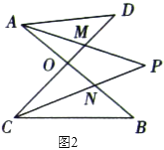
(1)在图![]() 中,请直接写出
中,请直接写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系:__________
之间的数量关系:__________
(2)仔细观察,在图![]() 中“
中“![]() ”字形的个数:______个;
”字形的个数:______个;
(3)图![]() 中,当
中,当![]() 度,
度,![]() 度时,求
度时,求![]() 的度数.
的度数.
(4)图![]() 中
中![]() 和
和![]() 为任意角时,其它条件不变,试问
为任意角时,其它条件不变,试问![]() 与
与![]() 、
、![]() 之间存在着怎样的数量关系?(直接写出结果,不必证明)
之间存在着怎样的数量关系?(直接写出结果,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC,EC分别为正方形ABCD和正方形EFCG的对角线,点E在△ABC内,连接BF,∠CAE+∠CBE=90°.

(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD 的边长为4,E 为AB 上一点,且AE=3 ,F 为BC 边上的一个动点,连接EF ,以EF 为边向左侧作等腰直角三角形FEG ,EG=EF,∠GEF=90°,连接AG ,则AG 的最小值为________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com