
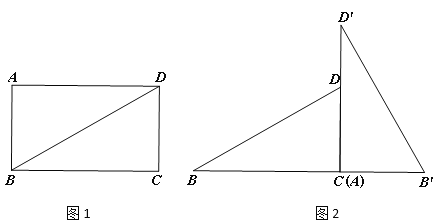
【题目】如图1,矩形ABCD,AB=4,BC=![]() .
.
(1)直接写出:∠ABD=______度;
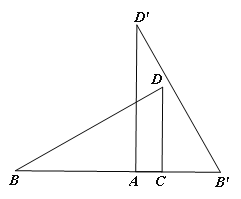
(2)将矩形ABCD沿BD剪开得到两个三角形,按图2摆放:点A与点C重合,CD落在AD′上,直接写出BD与B′D′的关系:_____;
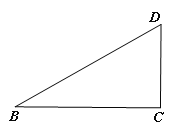
(3)在图2的基础上将△AB′D′向左平移,点B′与B重合停止,设AC=x,两个三角形重合部分的封闭图形的周长为y,请用x表示y:____.
【答案】60 BD=B′D′,BD⊥B′D′ 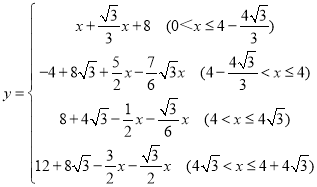
【解析】
(1)解直角三角形即可解决问题.
(2)结论:BD⊥B′D′,BD=B′D′.利用“8字型”证明∠DHD′=∠BAD=90°即可.
(3)分四种情形①如图3-1中,当0<x≤![]() 时,重叠部分是四边形ACDH.②如图3-2中,当
时,重叠部分是四边形ACDH.②如图3-2中,当![]() <x≤4时,重叠部分是五边形ACMNH.③如图3-2中,当
<x≤4时,重叠部分是五边形ACMNH.③如图3-2中,当![]() <x≤
<x≤![]() 时,重叠部分是五边形ACMNH.如图3-4中,当
时,重叠部分是五边形ACMNH.如图3-4中,当![]() <x<4+
<x<4+![]() 时,重叠部分是△BB′H.分别求解即可.
时,重叠部分是△BB′H.分别求解即可.
解:(1)如图1中,
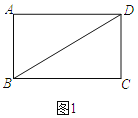
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=![]() ,
,
∴tan∠ABD=![]() ,
,
∴∠ABD=60°,
故答案为:60.
(2)结论:BD⊥B′D′,BD=B′D′.
理由:如图2中,延长BD交D′B′于H.
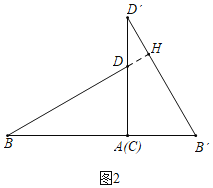
∵∠B=∠D′,∠BDA=∠HDD′,
∴∠BAD=∠DHD′=90°,
∴BD⊥B′D′.
∵BD与B′D′为矩形的对角线,则BD=B′D′;
故答案为:BD=B′D′,BD⊥B′D′.
(3)①如图3-1中,当0<x≤![]() 时,重叠部分是四边形ACDH,
时,重叠部分是四边形ACDH,
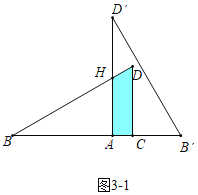
由题意:AB=![]() ,AH=
,AH=![]() AB=
AB=![]() ,
,
∵AH∥CD,
∴![]() ,
,
∴![]() ,
,
∴BH=![]() ,
,
∴DH=8-(![]() )=
)=![]() ,
,
y=x+4+![]()
=x+4+4![]()
=![]() ;
;
②如图3-2中,当![]() <x≤4时,重叠部分是五边形ACMNH.
<x≤4时,重叠部分是五边形ACMNH.
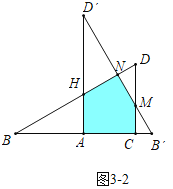
![]()
=![]()
=![]() ;
;
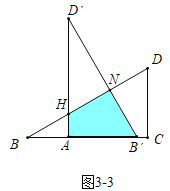
③如图3-3中,当4<x≤![]() 时,重叠部分是四边形AB′NH.
时,重叠部分是四边形AB′NH.
![]()
=![]()
=![]() ;
;
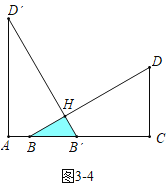
④如图3-4中,当![]() 时,重叠部分是△BB′H.
时,重叠部分是△BB′H.
![]()
![]()
![]() ;
;
故答案为: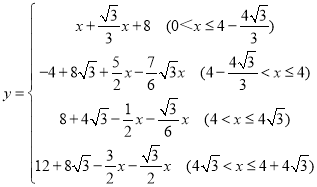 ;
;


科目:初中数学 来源: 题型:
【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )

①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣![]() x+1与y轴交于点D.
x+1与y轴交于点D.

(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
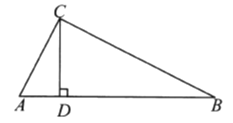
【题目】如图,在![]() 中,
中, ![]() ,CD是斜边AB上的高.
,CD是斜边AB上的高.
(1)证明: ![]() ∽
∽![]()
(2)写出除(1)外的另两对相似三角形.
(3)AC是哪两条线段的比例中项?请简要证明(说明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的对角线交于点E,将△DCB沿CD翻折得到△DCF.
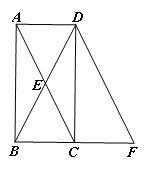
(1)求证:四边形ACFD是平行四边形;
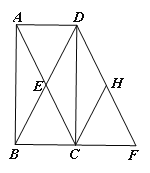
(2)点H为DF的中点,连结CH,若AB=4,BC=2,求四边形ECHD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC的三边长分别为6 cm、7.5 cm、9 cm,三角形DEF的一边长为4 cm.当三角形DEF的另两边长是下列哪一组时,这两个三角形相似( )
A. 2 cm、3 cm B. 4 cm、5 cm C. 5 cm、6 cm D. 6 cm、7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )

A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com