
【题目】如图,OF是∠MON的平分线,点A在射线OM上,P,Q是直线ON上的两动点,点Q在点P的右侧,且PQ=OA,作线段OQ的垂直平分线,分别交直线OF、ON交于点B、点C,连接AB、PB.
(1)如图1,当P、Q两点都在射线ON上时,请直接写出线段AB与PB的数量关系;
(2)如图2,当P、Q两点都在射线ON的反向延长线上时,线段AB,PB是否还存在(1)中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
(3)如图3,∠MON=60°,连接AP,设![]() =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
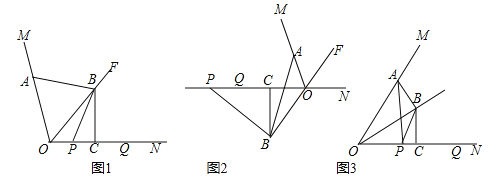
【答案】(1)AB=PB;(2)存在;(3)k=0.5.
【解析】试题分析:(1)结论:AB=PB.连接BQ,只要证明△AOB≌△PQB即可解决问题;
(2)存在.证明方法类似(1);
(3)连接BQ.只要证明△ABP∽△OBQ,即可推出![]() =
=![]() ,由∠AOB=30°,推出当BA⊥OM时,
,由∠AOB=30°,推出当BA⊥OM时, ![]() 的值最小,最小值为0.5,由此即可解决问题;
的值最小,最小值为0.5,由此即可解决问题;
试题解析:解:(1)连接:AB=PB.理由:如图1中,连接BQ.

∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∴∠AOB=∠BQO,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(2)存在,理由:如图2中,连接BQ.
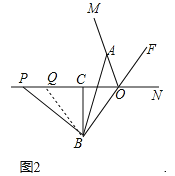
∵BC垂直平分OQ,∴BO=BQ,∴∠BOQ=∠BQO,∵OF平分∠MON,∠BOQ=∠FON,∴∠AOF=∠FON=∠BQC,∴∠BQP=∠AOB,∵OA=PQ,∴△AOB≌△PQB,∴AB=PB.
(3)连接BQ.
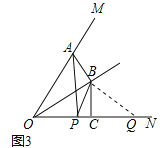
易证△ABO≌△PBQ,∴∠OAB=∠BPQ,AB=PB,∵∠OPB+∠BPQ=180°,∴∠OAB+∠OPB=180°,∠AOP+∠ABP=180°,∵∠MON=60°,∴∠ABP=120°,∵BA=BP,∴∠BAP=∠BPA=30°,∵BO=BQ,∴∠BOQ=∠BQO=30°,∴△ABP∽△OBQ,∴ ![]() =
=![]() ,∵∠AOB=30°,∴当BA⊥OM时,
,∵∠AOB=30°,∴当BA⊥OM时, ![]() 的值最小,最小值为0.5,∴k=0.5.
的值最小,最小值为0.5,∴k=0.5.
点睛:本题考查相似综合题、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.
【题型】解答题
【结束】
28
【题目】如图,已知抛物线y=ax2+![]() x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣![]() x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.

(1)试求该抛物线表达式;
(2)如图(1),若点P在第三象限,四边形PCOF是平行四边形,求P点的坐标;
(3)如图(2),过点P作PH⊥y轴,垂足为H,连接AC.
①求证:△ACD是直角三角形;
②试问当P点横坐标为何值时,使得以点P、C、H为顶点的三角形与△ACD相似?
【答案】(1)y=![]() x2+
x2+![]() x﹣4;(2)点P的坐标为(﹣
x﹣4;(2)点P的坐标为(﹣![]() ,﹣
,﹣![]() )或(﹣8,﹣4);(3)点P的横坐标为﹣5.5或﹣10.5或2或﹣18时,使得以点P、C、H为顶点的三角形与△ACD相似.
)或(﹣8,﹣4);(3)点P的横坐标为﹣5.5或﹣10.5或2或﹣18时,使得以点P、C、H为顶点的三角形与△ACD相似.
【解析】试题分析:(1)利用待定系数法列方程求解析式.(2)把P,F点坐标用m表示写出来,利用四边形PCOF是平行四边形得到m值,求得P点坐标.(3) ①由两点间的距离公式可知分别计算AC,CD,AD勾股定理逆定理知三角形是直角三角形;②分类讨论,△ACD∽△CHP,△ACD∽△PHC分别计算P点坐标.
试题解析:
解:(1)由题意得: 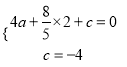 ,解得:
,解得: 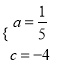 ,
,
∴抛物线的表达式为y=![]() x2+
x2+![]() x﹣4.
x﹣4.
(2)设P(m, ![]() m2+
m2+![]() m﹣4),则F(m,﹣
m﹣4),则F(m,﹣![]() m﹣4).
m﹣4).
∴PF=(﹣![]() m﹣4)﹣(
m﹣4)﹣(![]() m2+
m2+![]() m﹣4)=﹣
m﹣4)=﹣![]() m2﹣
m2﹣![]() m.
m.
∵PE⊥x轴,
∴PF∥OC.
∴PF=OC时,四边形PCOF是平行四边形.
∴﹣![]() m2﹣
m2﹣![]() m=4,解得:m=﹣
m=4,解得:m=﹣![]() 或m=﹣8.
或m=﹣8.
当m=﹣![]() 时,
时, ![]() m2+
m2+![]() m﹣4=﹣
m﹣4=﹣![]() ,
,
当m=﹣8时, ![]() m2+
m2+![]() m﹣4=﹣4.
m﹣4=﹣4.
∴点P的坐标为(﹣![]() ,﹣
,﹣![]() )或(﹣8,﹣4).
)或(﹣8,﹣4).
(3)①证明:把y=0代入y=﹣![]() x﹣4得:﹣
x﹣4得:﹣![]() x﹣4=0,解得:x=﹣8.
x﹣4=0,解得:x=﹣8.
∴D(﹣8,0).
∴OD=8.
∵A(2,0),C(0,﹣4),
∴AD=2﹣(﹣8)=10.
由两点间的距离公式可知:AC2=22+42=20,DC2=82+42=80,AD2=100,
∴AC2+CD2=AD2.
∴△ACD是直角三角形,且∠ACD=90°.
②由①得∠ACD=90°.
当△ACD∽△CHP时, ![]() ,即
,即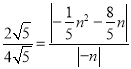 ,
,
解得:n=0(舍去)或n=﹣5.5或n=﹣10.5.
当△ACD∽△PHC时, ![]() ,即
,即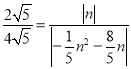 ,
,
解得:n=0(舍去)或n=2或n=﹣18.
综上所述,点P的横坐标为﹣5.5或﹣10.5或2或﹣18时,使得以点P、C、H为顶点的三角形与△ACD相似.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
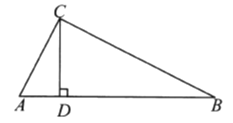
【题目】如图,在![]() 中,
中, ![]() ,CD是斜边AB上的高.
,CD是斜边AB上的高.
(1)证明: ![]() ∽
∽![]()
(2)写出除(1)外的另两对相似三角形.
(3)AC是哪两条线段的比例中项?请简要证明(说明).
查看答案和解析>>
科目:初中数学 来源: 题型:
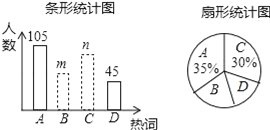
【题目】2017年3月全国两会胜利召开,某学校就两会期间出现频率最高的热词:A.蓝天保卫战,B.不动产保护,C.经济增速,D.简政放权等进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】终身学习是学习型社会的核心内容,努力建设“学习型家庭”也是一个重要组成部分.为了解“学习型家庭”情况,某社区对部分家庭六月份的平均每天看书学习时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
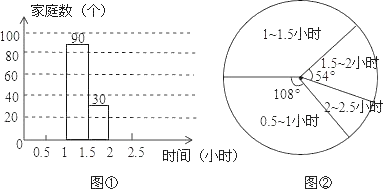
(1)本次抽样调查了多少个家庭;
(2)将图①中的条形图补充完整;
(3)学习时间在1~1.5小时的部分对应的扇形圆心角的度数是多少;
(4)若该社区有家庭有5000个,请你估计该社区学习时间不少于1小时的约有多少个家庭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )

A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年我市的脐橙喜获丰收,脐橙一上市,水果店的陈老板用2400元购进一批脐橙,很快售完;陈老板又用6000元购进第二批脐橙,所购件数是第一批的2倍,但进价比第一批每件多了20元.
(1)第一批脐橙每件进价多少元?
(2)陈老板以每件120元的价格销售第二批脐橙,售出60%后,为了尽快售完,决定打折促销,要使第二批脐橙的销售总利润不少于480元,剩余的脐橙每件售价最低打几折?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①为Rt△AOB,∠AOB=90°,其中OA=3,OB=4.将AOB沿x轴依次以A,B,O为旋转中心顺时针旋转.分别得图②,图③,…,则旋转到图⑩时直角顶点的坐标是_____.
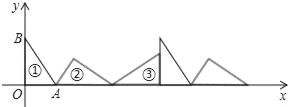
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com