
【题目】如图,△ABC中,∠C=90°,AC=BC,AD=16cm,BE=12cm,点P是斜边AB的中点.有一把直角尺MPN,将它的顶点与点P重合,将此直角尺绕点P旋转,与两条直角边AC和CB分别交于点D和点E.则线段PD和PE的数量关系为_____,线段DE=_____cm.

科目:初中数学 来源: 题型:
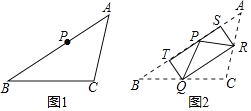
【题目】如图所示,图1为三角形纸片ABC,点P在AB上.若将纸片向内折叠,如图2所示,点A、B、C恰能重合在点P处,折痕分别为SR、RQ、QT,折痕的交点R、Q分别在边AC、BC上.若△ABC、四边形PTQR的面积分别是20和7,则△RPS的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江津四面山是国家5A级风景区,里面有一个景点被誉为亚洲第一岩﹣﹣土地神岩,土地神岩壁画高度从石岩F处开始一直竖直到山顶E处,为了测量土地神岩上壁画的高度,小明从山脚A处,沿坡度i=0.75的斜坡上行65米到达C处,在C处测得山顶E处仰角为26.5°,再往正前方水平走15米到达D处,在D处测得壁画底端F处的俯角为42°,壁画底端F处距离山脚B处的距离是12米,A、B、C、D、E、F在同一平面内,A、B在同一水平线上,EB⊥AB,根据小明的测量数据,则壁画的高度EF为( )米(精确到0.1米,参考数据:sin26.5°≈0.45,cos26.5°≈0.9,tan26.5°≈0.5,sin42°≈0.67,cos42°≈0.74,tan42°≈0.9)

A. 49.5 B. 68.7 C. 69.7 D. 70.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△ADC≌△BOC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,判断△AOD的形状,并说明理由。
(3)探究:当α=_____度时,△AOD是等腰三角形。

查看答案和解析>>
科目:初中数学 来源: 题型:
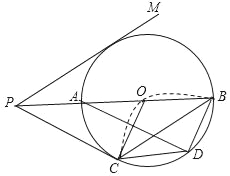
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
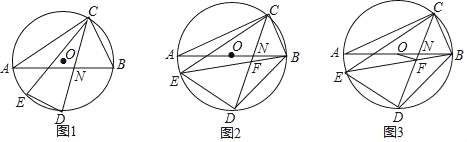
【题目】如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N.
(1)如图1,求证:∠AND=∠CED;
(2)如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°﹣∠DBE,求证:CD=CE;
(3)如图3,在(2)的条件下,连接OF,若BE=BD+4,BC=![]() ,求线段OF的长.
,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交![]() 轴于D点,过点D作DF⊥AE于点F。
轴于D点,过点D作DF⊥AE于点F。

(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)小明在解答本题时,发现△AOE是等腰三角形。由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”。你同意他的看法吗?请充分说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别是AD,BC的中点,AF与BE相交于点M,CE与DF相交于点N,QM⊥BE,QN⊥EC相交于点Q,PM⊥AF,PN⊥DF相交于点P,若2BC=3AB,记△ABM和△CDN的面积和为S,则四边形MQNP的面积为( )

A. ![]() S B.
S B. ![]() S C.
S C. ![]() S D.
S D. ![]() S
S
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com