Question

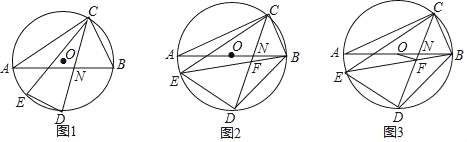
【题目】如图，△ABC内接于⊙O，弦CD平分∠ACB，点E为弧AD上一点，连接CE、DE，CD与AB交于点N．

（1）如图1，求证：∠AND=∠CED；

（2）如图2，AB为⊙O直径，连接BE、BD，BE与CD交于点F，若2∠BDC=90°﹣∠DBE，求证：CD=CE；

（3）如图3，在（2）的条件下，连接OF，若BE=BD+4，BC=，求线段OF的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）OF=.

【解析】

（1）连接BE，则∠CAB=∠CEB，∠BCD=∠DEB，由CD是∠ACB的平分线得∠ACD=∠BCD，从而，∠CAB+∠ACD=∠CEB+∠DEB；由∠CAB+∠ACD=∠AND可得结论；

（2）根据2∠BDC=90°-∠DBE得∠BDC+∠DBE=90°-∠BDC，由∠BDC=∠BAC得∠BDC+∠DBE=∠CFB，结合AB是直径可得∠CFB=∠CBN，从而可证明∠CDE=∠CED，故可得结论；

（3）过C作CM⊥BE，CK⊥DB易证△CEM≌△CDK，△CMB≌△CKB从而求出CM=6，作FH⊥BC于点H,FH交CM于点G，易证△CGH≌△FHB，得CG=BF，设FM=x，利用tan∠GFM=tan∠MCB==求得 FM=3,CF=3. 作EQ⊥DF交DF于点Q，通过△CBF∽△EDF设FQ=3k，EQ==6k，则DQ=2k,EF=3k，DE=2k得BE=5+3k，BD=BE-4=3k+1，作DP⊥BE交于点P，运用勾股定理求出k的值，连接OD,在Rt△ODF中,OF2=OD2 -DF2=50-45=5，故OF=.

(1)证明：连接BE.

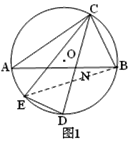
∠CED=∠CEB+∠DEB

∠AND=∠CAB+∠ACD

∵CD是∠ACB的平分线

∴∠ACD=∠BCD=∠DEB

∵∠CAB=∠CEB，

∴∠CAB+∠ACD=∠CEB+∠DEB

∠CED=∠AND；

(2)∵2∠BDC=90-∠DBE

∴∠BDC+∠DBE=90°-∠BDC

∵∠BDC=∠BAC

∴∠BDC+∠DBE=∠CFB

∴90°-∠DBE=90°-∠CAB

∵AB是直径，∴∠ACB=90

∴∠CFB=∠CBN，

∠CNB=∠CBE=∠CDE

∠CNB=∠AND=∠CED

∴∠CDE=∠CED，

∴CE=CD；

(3)过C作CM⊥BE，CK⊥DB

∴∠CME=∠CKD=90°，∠CEM=∠CDK，CE=CD

∴△CEM≌△CDK，∴EM=DK，CM=CK

∴△CMB≌△CKB，∴BM=BK

∴BE-BD=2BM=4，BM=2，∴CM=6.；

作FH⊥BC于点H,FH交CM于点G

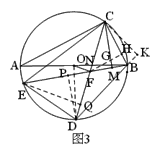
∵∠FCB=45°∴△CGH≌△FHB，∴CG=BF

设FM=x，∴CG=BF=x+2，GM=6-(x+2)=4-x

tan∠GFM=tan∠MCB==

∴x=3,FM=3,CF=3.

∵△CBF∽△EDF(可以用正切值相等)

作EQ⊥DF交DF于点Q

设FQ=3k，EQ==6k，则DQ=2k,EF=3k，DE=2k

∴BE=5+3k，BD=BE-4=3k+1

作DP⊥BE交于点P,∵∠PED=∠BCD=45°,

∴PD=PE=DE=2k,PB=BE-PE=5+k；

在Rt△PDB中，PB2+PD2=DB2,(5+k)2+(2k)2=(3k+1)2

∴k=, DF=5k=3=CF, BD=3k+1=10,；

∴OF⊥CD

连接OD,∴∠AOD=∠BOD=90°,∴OD=BD=5

在Rt△ODF中,OF2=OD2 -DF2=50-45=5，∴OF=