
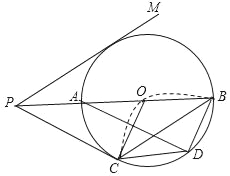
【题目】如图,AB为⊙O的直径,点C为⊙O上一点,将弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,连接OC,CD,BD,过点C的切线与线段BA的延长线交于点P,连接AD,在PB的另一侧作∠MPB=∠ADC.
(1)判断PM与⊙O的位置关系,并说明理由;
(2)若PC=![]() ,求四边形OCDB的面积.
,求四边形OCDB的面积.
【答案】(1)PM与⊙O相切,理由见解析;(2)![]() .
.
【解析】
(1)连接DO并延长交PM于E,如图,利用折叠的性质得OC=DC,BO=BD,则可判断四边形OBDC为菱形,所以OD⊥BC,△OCD和△OBD都是等边三角形,从而计算出∠COP=∠EOP=60°,接着证明PM∥BC得到OE⊥PM,所以OE=![]() OP,根据切线的性质得到OC⊥PC,则OC=
OP,根据切线的性质得到OC⊥PC,则OC=![]() OP,从而可判定PM是⊙O的切线;
OP,从而可判定PM是⊙O的切线;
(2)先在Rt△OPC中计算出OC=1,然后根据等边三角形的面积公式计算四边形OCDB的面积.
(1)PM与⊙O相切.
理由如下:连接DO并延长交PM于E,如图,
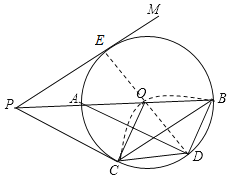
∵弧BC沿直线BC翻折,使弧BC的中点D恰好与圆心O重合,
∴OC=DC,BO=BD,
∴OC=DC=BO=BD,
∴四边形OBDC为菱形,
∴OD⊥BC,
∴△OCD和△OBD都是等边三角形,
∴∠COD=∠BOD=60°,
∴∠COP=∠EOP=60°,
∵∠MPB=∠ADC,
而∠ADC=∠ABC,
∴∠ABC=∠MPB,
∴PM∥BC,
∴OE⊥PM,
∴OE=![]() OP,
OP,
∵PC为⊙O的切线,
∴OC⊥PC,
∴OC=![]() OP,
OP,
∴OE=OC,
而OE⊥PC,
∴PM是⊙O的切线;
(2)在Rt△OPC中,OC=![]() PC=
PC=![]() ,
,
∴四边形OCDB的面积=2S△OCD=2×![]() ×12=
×12=![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点D在△ABC的边AB上,且AD=CD,
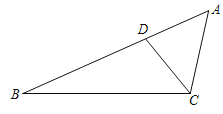
(1)用直尺和圆规作∠BDC的平分线DE,交BC于点E(不写作法,保留作图痕迹);
(2)在(1)的条件下,判断DE与AC的位置关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出m= ,n= ;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生中,大约有多少人最认可“微信”这一新生事物?
(4)已知A、B两位同学都最认可“微信”,C同学最认可“支付宝”D同学最认可“网购”从这四名同学中抽取两名同学,请你通过树状图或表格,求出这两位同学最认可的新生事物不一样的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九龙坡区某社区开展全民读书活动,以丰富人们业余文化生活现计划筹资30000元用于购买科普书籍和文艺刊物
(1)计划购买文艺刊物的资金不少于购买科普书籍资金的2倍,那么最少用多少资金购买文艺刊物?
(2)经初步了解,有200户居民自愿参与集资,那么平均每户需集资150元.经筹委会进步宣传,自愿参加的户数在200户的基础上增加了a%(其中a>50),如果每户平均集资在150元的基础上减少![]() a%,那么实际筹资将比计划筹资多6000元,求a的值.
a%,那么实际筹资将比计划筹资多6000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD=16cm,BE=12cm,点P是斜边AB的中点.有一把直角尺MPN,将它的顶点与点P重合,将此直角尺绕点P旋转,与两条直角边AC和CB分别交于点D和点E.则线段PD和PE的数量关系为_____,线段DE=_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,BD是AC上的高线.作AE⊥AB于点A,交BD的延长线于点E.取BE的中点M,连结AM.

(1)求证:△AEM是等边三角形;
(2)若AE=2,求△AEM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
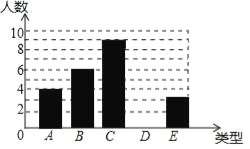
【题目】某校初一年级随机抽取30名学生,对5种活动形式:A、跑步,B、篮球,C、跳绳,D、乒乓球,E、武术,进行了随机抽样调查,每个学生只能选择一种运动行驶,调查统计结果,绘制了不完整的统计图.
(1)将条形图补充完整;
(2)如果初一年级有900名学生,估计喜爱跳绳运动的有多少人?
(3)某次体育课上,老师在5个一样的乒乓球上分别写上A、B、C、D、E,放在不透明的口袋中,每人每次摸出一个球并且只摸一次,然后放回,按照球上的标号参加对应活动,小明和小刚是好朋友,请用树状图或列表法的方法,求他俩恰好是同一种活动形式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( )

A.1对B.2对C.3对D.4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com